固定座標系から回転座標系に運動方程式を変換すると,慣性力である遠心力とコリオリ力が数式的に現れます。計算は面倒ですが,いったんできるようになるとおトクだと思います。
座標の変換を図で理解する
ここでは簡単のために2次元平面上での運動方程式を考えます。大学初年次で扱うレベルの古典物理では2次元が多い気がするので,とりあえずこれでいいでしょう。
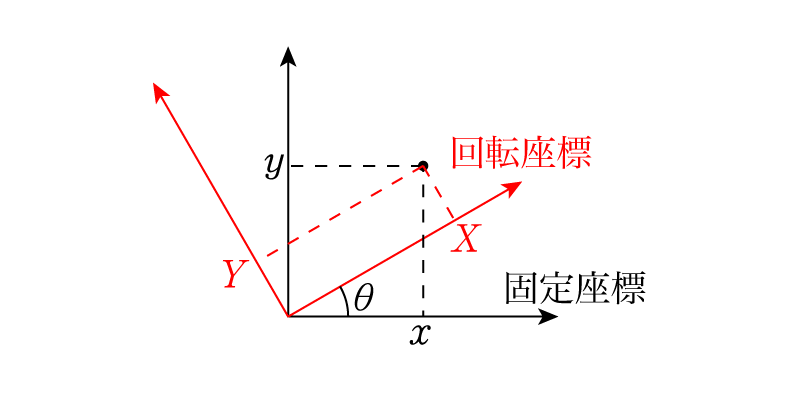
黒い座標が固定されていて,赤い座標は角速度\(\omega\)で時計回りに回転しているとしましょう。固定座標で\((x,y)\)と表される点が,回転座標で\((X,Y)\)と表されるとき,\begin{align} \begin{pmatrix} x \\ y \end{pmatrix} &= \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} X \\ Y \end{pmatrix} \\ &= \begin{pmatrix} X\cos\theta-Y\sin\theta \\ X\sin\theta + Y\cos\theta \end{pmatrix} \end{align}という等式が成立します。回転→固定に座標変換するとき,座標軸が\(-\theta\)だけ回転しているので,点の座標は\(\theta\)回転をします。ゆえにその回転行列\(R(\theta)\)をかければ\((x,y)\)を\((X,Y)\)で表すことができます。
別の方法として,現行課程の高校生向けの複素数を使う方法も紹介しておきます。上の図を複素数平面だと思うと,\(X+iY\)から\(x+iy\)に変換するために\(\theta\)回転を表す\(\cos\theta + i\sin\theta\)をかければ良いです。つまり
です。実部と虚部を対応させれば同じになりますね。
同様に回転座標系での速度をそれぞれ\[ \quad v_X = \dfrac{dX}{dt}, \quad v_Y = \dfrac{dY}{dt}\]と書くことにすると,これも回転行列をかけることにより固定座標系での速度\(v_x, v_y\)は\[ \begin{pmatrix} v_x \\ v_y \end{pmatrix} = \begin{pmatrix} v_X\cos\theta-v_Y\sin\theta \\ v_X\sin\theta + v_Y\cos\theta \end{pmatrix} \]です。
また回転座標系での加速度をそれぞれ次のように書くと\[ a_X = \dfrac{d^2X}{dt^2}, \quad a_Y = \dfrac{d^2Y}{dt^2}\]固定座標系での加速度\(a_x, a_y\)は\[ \begin{pmatrix} a_x \\ a_y \end{pmatrix} = \begin{pmatrix} a_X\cos\theta-a_Y\sin\theta \\ a_X\sin\theta + a_Y\cos\theta \end{pmatrix} \]とわかります。
運動方程式の変換
いよいよこの回転座標系での運動方程式を求めます。固定座標系での運動方程式は,\[ m\dfrac{d^2 x}{dt^2} = F_x, \quad m\dfrac{d^2 y}{dt^2} = F_y \tag{$\ast$}\]です。この式の右辺に前節で求めた変換式を代入して計算していくことで,回転座標系での運動方程式を求めることができます。なお,回転座標系は一定の角速度\(\omega\)で回っているとするので\[ \dfrac{d\theta}{dt} = \omega\]となります。まずは\(x\)について,
\dfrac{d^2x}{dt} &= \dfrac{d}{dt} \left\{ \dfrac{d}{dt} ( X\cos\theta-Y\sin\theta) \right\} \\
&= \dfrac{d}{dt} \left( \cos\theta \dfrac{dX}{dt}-\omega X\sin\theta-\sin\theta \dfrac{dY}{dt}-\omega Y\cos\theta \right) \\
&= \left( \cos\theta \dfrac{d^2X}{dt^2}-\sin\theta \dfrac{d^2Y}{dt^2} \right)-2\omega \left( \sin\theta \dfrac{dX}{dt} + \cos\theta \dfrac{dY}{dt} \right)-\omega^2 (X\cos\theta-Y\sin\theta) \\
&= (a_X \cos\theta-a_Y \sin\theta)-2\omega(v_X \sin\theta + v_Y\cos\theta)-\omega^2 (X\cos\theta-Y\sin\theta)
\end{align}
\dfrac{d^2y}{dt} &= \dfrac{d}{dt} \left\{ \dfrac{d}{dt} ( X\sin\theta + Y\cos\theta) \right\} \\
&= \dfrac{d}{dt} \left( \sin\theta \dfrac{dX}{dt} + \omega X\cos\theta + \cos\theta \dfrac{dY}{dt}-\omega Y\sin\theta \right) \\
&= \left( \sin\theta \dfrac{d^2X}{dt^2} + \cos\theta \dfrac{d^2Y}{dt^2} \right) + 2\omega \left( \cos\theta \dfrac{dX}{dt}-\sin\theta \dfrac{dY}{dt} \right)-\omega^2 (X\sin\theta + Y\cos\theta) \\
&= (a_X \sin\theta + a_Y \cos\theta) + 2\omega(v_X \cos\theta-v_Y\sin\theta)-\omega^2 (X\sin\theta + Y\cos\theta)
\end{align}
F_x &= (a_X \cos\theta-a_Y \sin\theta)-2\omega(v_X \sin\theta + v_Y\cos\theta)-\omega^2 (X\cos\theta-Y\sin\theta) \tag{1} \\
F_y &= (a_X \sin\theta + a_Y \cos\theta) + 2\omega(v_X \cos\theta-v_Y\sin\theta)-\omega^2 (X\sin\theta + Y\cos\theta) \tag{2} \end{align}
\((1) \times (-\sin\theta) + (2) \times \cos\theta\)で左辺が\(F_Y\)
- 第1項:回転座標系でみた力
- 第2項:コリオリ力
- 第3項:遠心力
第1項の力以外に2つの慣性力(見かけ上の力)が生じています。固定座標系では「位置の二階微分=加速度」でしたが,回転座標系という非慣性系ではこのような力が生じることとなりますので,それぞれについて説明していきます。
コリオリ力
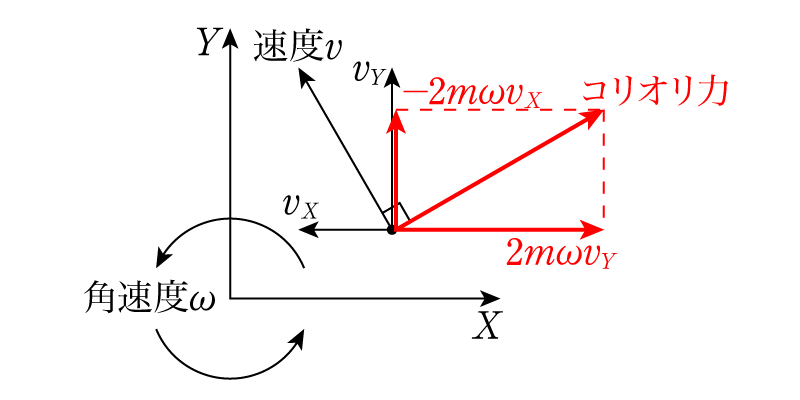
このコリオリ力と呼ばれる慣性力は\[(2m\omega v_Y, -2m\omega v_X)\]と表されるため,回転座標系の中で速度\((v_X,v_Y)\)を持っているときに見かけ上生じる力です。その向きは\(\omega > 0\)(反時計回り)であれば下の図に表されるように速度の方向に向かって右手側になります。
数学的にはこれで良いのですが,少しわかりづらいので次のような例を考えてみましょう。回転円盤の上に座標\(X,Y\)を原点を回転軸に固定しておいて,原点からある時刻に\(X\)軸正方向にボールを打ち出したとしましょう。
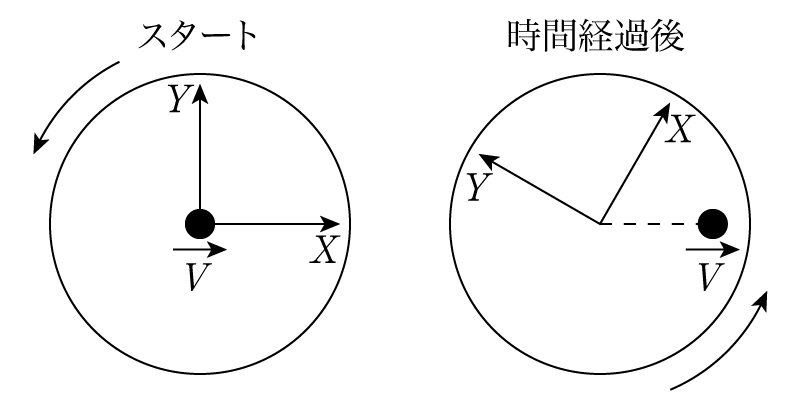
速度\(V\)で打ち出された球は何の力も受けないはずですから,回転円盤の外側から見れば,横方向に動き続けます。ですが,回転円盤上の座標軸は時間とともに回転していきます。そのため,回転座標上で見ると\(X\)軸上を直線運動するのではなく,ボールの進行方向向かって右側に力を受けたようにそれていくことがわかります。この力はあくまで座標軸が回転しているために,軌道がそれているだけで,本当は何の力もかかっていないことがわかると思います。
遠心力
これは日常的にも使われる力で実感することも多いと思います。一言で言えば,回転中心から遠ざかるように受ける力のことですが,その正体もまた座標軸が回転することにより存在するように見える架空の力です。その力は\[ (m\omega^2 X, m\omega^2 Y)\]となりますから,生じる加速度は角速度の二乗・中心からの距離に比例します。もちろんこの力には速度が入っていませんから,物体が動いてようが止まっていようが,原点にいる時以外は必ず受ける力です。
この回転座標系において現れるコリオリ力と遠心力は,常に回転している地球上での物理現象を考えるときに非常に重要な役割を果たします。コリオリ力は実際の生活で実感することはほとんどないですが,地球上の大気の流れを理解するには必要不可欠なものです。またどっかのタイミングでその話はまとめて記事にしたいと思います。

コメント