高校物理で出てくる「万有引力」という力。この世界における非常に普遍的な力で,これによって多くの自然界における法則を導くこともできる強力なものです。その定義から性質まで確認していきましょう。
万有引力とは何か
まずこの万有引力という力ですが,以下のように説明することができます。
- 質量を持つ2つの物体同士に必ず働く力
- 力の大きさは2物体の質量に比例し,距離の2乗に反比例する
- 力の向きはお互いを引きあう方向(引力)
図にすると次のようになります。
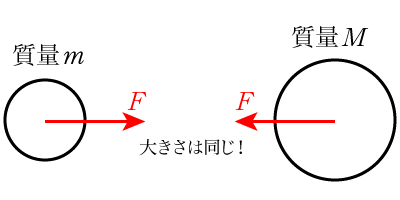
異なる質量の物体に働く力でも大きさは同じ\(F\)であることに注意してくださいね。さて気になるのは,この力の大きさですが,次のように書けます。
ここで,\(r\)は2物体の距離で,\(G\)は万有引力定数といって比例定数の役割を持っています。その値はおよそ\(6.67\times10^{-11} \, \mathrm{m^3/(kg \cdot s^2)}\)です。あまりこの値を使って問題を解くということは無いですが,興味のある人は頭の片隅に入れとくと良いですね。
万有引力の値の具体例
上述したものはただの定義で,「ああそうですか」となってしまうと思うので,いくつか具体的な値を出してみましょう。例えば
- 太陽の質量:\( 2.0 \times 10^{30} \mathrm{kg} \)
- 地球の質量:\( 6.0 \times 10^{24} \mathrm{kg} \)
- 太陽と地球の距離:\( 1.5 \times 10^{11} \mathrm{m} \)
を用いて,地球が太陽から受ける万有引力を計算してみると,その大きさ\(F\)は
F &= 6.67\times10^{-11} \, \mathrm{m^3/(kg \cdot s^2)} \times \dfrac{ 2.0 \times 10^{30} \mathrm{kg} \times 6.0 \times 10^{24} \mathrm{kg} }{ (1.5 \times 10^{11} \mathrm{m})^2 } \\ &= 3.6 \times 10^{21} \mathrm{N}
\end{align}
と求まります。非常に大きい力で引き合っていることがわかりますね。
一方で,\(G\)の値が非常に小さいことに気が付いたでしょうか。10のマイナス11乗という比例定数ですから,質量がよほど大きくないとほとんど力がないことがわかりますね。日常生活でも我々人間同士や物同士(冷蔵庫と電子レンジとか)も引き合っていますが,質量が\(G\)に比してかなり小さいことから目に見えるほどの力は生じていないんですね。
次に地球表面にある1kgの物体と地球の間の万有引力を考えてみましょう。物体間の距離は物体の重心間の距離と考えてよいから,この場合の物体と地球の距離は地球の半径ですね(表面にいるからと言ってゼロではありません!)。地球の半径はだいたい\( 6.4 \times 10^6 \mathrm{m} \)だから,力の大きさは
F &= 6.67\times10^{-11} \, \mathrm{m^3/(kg \cdot s^2)} \times \dfrac{ 1 \mathrm{kg} \times 6.0 \times 10^{24} \mathrm{kg} }{ (6.4 \times 10^{6} \mathrm{m})^2 } \\ &= 9.8 \, \mathrm{N}
\end{align}
となります。どこかでこの値見たことありませんか。これは重力加速度\(g\)と同じ値ですね!1kgの物体が受ける重力の大きさは\(g\)でしたから,確かにその値が出てきました。つまり地球上の物体にかかる重力とは地球から受ける万有引力だったのです。
万有引力による位置エネルギー
質量\(m\)の物体(例えば地球)が質量\(M\)の物体(例えば太陽)から距離\(r\)だけ離れているとき,お互いが位置エネルギーを持っています。まずはその式の形を頭にいれましょう。位置エネルギー\(U\)は以下のように書けます。
- マイナスの値であること
- 距離そのものに反比例すること
という点で異なります。位置エネルギーについてよく知っている人は「位置エネルギーって基準をどこにとるかで変わるんじゃないの?」と思うでしょうが,万有引力については基準を無限遠方に取ることが通例です。はるか無限のかなたで位置エネルギーがゼロであるとしたときの位置エネルギーが上の式で表されます。実際に具体例を使って考えてみましょう。
万有引力が働く下でのエネルギー保存
高校での試験や大学入試では上述の力・エネルギーの式を覚えるだけでなく,使いこなすことを要求されますが,多くの場合エネルギー保存を用いて考えます。次のような例を考えてみましょう。
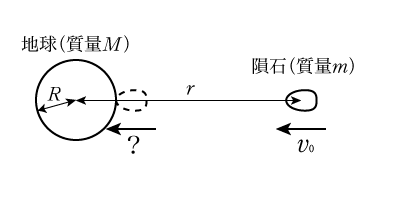
かなり激ヤバな状況ですが,地球に隕石が向かっていて,距離\(r\)離れているときの速さが\(v_0\)だとわかったとき,地球に衝突する瞬間の速さを求めてみましょう。なお,隕石の大きさは無視します。距離離れているときの力学的エネルギーは
\[ \dfrac{1}{2}m{v_0}^2 – G\dfrac{Mm}{r} \]
です。もちろん一つ目が運動エネルギー,二つ目が位置エネルギーです。衝突する瞬間の力学的エネルギーは,衝突時の速さを\(v\)とすると
\[ \dfrac{1}{2}m{v}^2 – G\dfrac{Mm}{R} \]
です。万有引力のみが働いているとき力学的エネルギーの和は一定なので,
\[ \dfrac{1}{2}m{v_0}^2 – G\dfrac{Mm}{r} = \dfrac{1}{2}m{v}^2 – G\dfrac{Mm}{R} \]
と立式できます。これを\(v\)について解くと,
\[ v = \sqrt{ {v_0}^2 + 2GM \left( \dfrac{1}{R} – \dfrac{1}{r} \right) } \]
と求めることができました。かっこの中身は正ですから,地球に近づいてくるにつれて隕石が加速していくことがわかりましたね!(だから何だって話ですが,100%助からないので)
ケプラーの法則
いよいよ万有引力により導かれる惑星運動についての法則に入ります。ケプラーの法則は3つあり,
- 惑星は太陽を焦点の一つとする楕円軌道上を公転する
- それぞれの惑星で面積速度は一定である
- 全ての惑星で公転周期\(T\)と回転長半径\(a\)について,\(\dfrac{T^2}{a^3}\)の値は一定
というものです。別に太陽系でなくとも太陽系と同じように恒星の周りを惑星が回っていれば成立するのですが,最初にケプラーが見つけたのは太陽系についてでした。それぞれ見ていきましょう。
惑星は太陽を焦点の一つとする楕円軌道上を公転する
この文言を聞いただけでは良くわからないと思うので,図を見てみてください。

惑星は太陽の周りをきれいな円を描いて回っているわけではありません。実は少しゆがんだ楕円なのです。ただし地球は特に長半径と短半径の差が非常に小さく,ほとんど円軌道を描いているといってよいくらいです。図にある2つの端点ですが,
- 近日点:太陽との距離が最も近い場所
- 遠日点:太陽との距離が最も遠い場所
というように定義されます。
それぞれの惑星で面積速度は一定である
面積速度なんて随分と聞きなれない言葉ですよね?この分野でしか用いられない単語だと思いますが,
\[ \text{面積速度} = \dfrac{1}{2}rv\sin\theta \]
で定義されます。特に,惑星が近日点や遠日点にあるとき,\(\theta=90^{\circ}\)だから面積速度は\(\dfrac{1}{2}rv\)と簡素化されます。これが常に一定であるというのが,この性質の主張です。
全ての惑星で公転周期\(T\)と回転長半径\(a\)について,\(\dfrac{T^2}{a^3}\)の値は一定
太陽系の中の全ての惑星で公転周期の2乗と回転長半径の3乗が比例するということを意味します。太陽系の場合は便利な方法があって,
- \(T\)の単位を年とする
- \(a\)の単位を天文単位とする
というルールにすると\(\dfrac{T^2}{a^3}\)の値は1となります。というのも
まとめ
万有引力の力の大きさ,位置エネルギー,またそれにより出てくるケプラーの法則はすべて確実に頭にいれましょう。ケプラーの法則は万有引力及び運動方程式から導出することもできますが,数学Ⅲの知識が必要になるので,興味のある人のみ取り組めばよいと思います。

コメント