高校物理の力学で1つの大きなテーマとなる2体問題。大学入試ではよく衝突・分裂前後の各物体の速度について議論がなされますが,それをエネルギーという観点から見直してみます。
今回考える状況
非常によくあるシチュエーションですが,次のような状況を考えてみます。質量\(m_1, m_2\)の2物体が右向き正とした速度\(v_1, v_2\)で衝突し,その後それぞれの速度が\(v’_1, v’_2\)になって運動していくとします。もちろん左向きに動いていてもいいのですが,その際は速度は負となります。
特に今回は議論を簡単にするために,また高校物理の範疇に収めるために,1次元の運動のみを考えます。
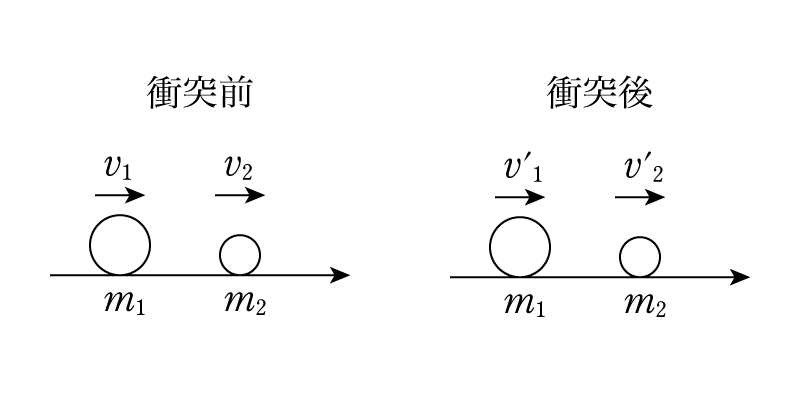
この衝突における反発係数(はねかえり係数)を\(e\)と書きます。つまり,\[ e = -\dfrac{v_2-v_1}{v’_2-v’_1} \]です。
運動エネルギーの合計値
この2物体の衝突前の運動エネルギーを単純に合計すると\[ \dfrac{1}{2}m_1 {v_1}^2 + \dfrac{1}{2}m_2 {v_2}^2 \tag{1} \]となります。今回はこれを少し工夫して変形してみます。下の式を見てみてください。
なんだかすごくごちゃごちゃしていますが,実はこの長い式は(展開して整理すればわかりますが)2物体の運動エネルギーの合計値\((1)\)と等しいです。この複雑にも見える変形には意味があり,それぞれの項にきちんと名前がつけられています。
- 第1項:重心運動エネルギー
- 第2項:相対運動エネルギー
2物体の運動エネルギーをそれぞれの物体の運動エネルギーの合計ではなく,重心運動と相対運動に分解して考える,という見方をしています。詳しくそれぞれのエネルギーについてみていきます。
重心運動エネルギー
2物体の重心運動エネルギー\(E_G\)は次のように定義されます。\[ E_G = \dfrac{1}{2} (m_1+m_2) \left( \dfrac{m_1v_1 + m_2v_2}{m_1+m_2} \right)^2\]この項を分解して解釈すると,\[ E_G = \dfrac{1}{2} \times 全質量 \times {重心速度}^2\]とみることができます。ここで重心速度は全運動量を全質量で割ったもので\[ 重心速度 = \dfrac{m_1v_1 + m_2v_2}{m_1+m_2}\]と定義されます。確かに一般的な運動エネルギーの形をしていますね。
この重心運動エネルギーの意味は,2物体の質量が全て重心に集まって重心速度で運動している,とした時の運動エネルギーです。ある意味重心速度とは各物体の速度を質量で重みをとった加重平均とも取れますから,その速度で全質量が動いている,と考えることでこの運動エネルギーが出てきます。
相対運動エネルギー
2物体の相対運動エネルギー\(E_R\)は次のように定義されます。\[ E_R = \dfrac{1}{2} \cdot \dfrac{m_1m_2}{m_1+m_2} (v_2-v_1)^2\]この項を分解して解釈すると,\[E_R = \dfrac{1}{2}\times 換算質量\times {相対速度}^2 \]とみることができます。ここで換算質量(\(\mu\)と書かれることが多い)は質量の積を質量の和で割ったもので,\[ \mu = \dfrac{m_1m_2}{m_1+m_2}\]と定義されます。少しややこしいですが,質量の2乗を質量で割っているので,単位は質量ですね。
この相対運動エネルギーの意味は,2物体がお互いに対して速度を持っている分のエネルギーです。上述の重心運動エネルギーでは,2つが重心の位置で一緒になって動いていると捉えたわけですが,もちろんお互いが別々の速度を持つときだってあります。そのような場合は\(v_2-v_1 \neq 0\)となりますから,この相対運動エネルギーが生じることとなります。
衝突前後のエネルギー変化
よく問題になるこのエネルギー変化。衝突の前後でエネルギーが増えることはないですが(もしあるなら永久機関を作り出せます),エネルギーは保存されるか減少します。これを考えていきましょう。衝突後の運動エネルギーの合計値は\[ \dfrac{1}{2}m_1 {v’_1}^2 + \dfrac{1}{2}m_2 {v’_2}^2 \tag{2} \]とかけるから,衝突によるエネルギー損失(減少量)は\((1)-(2)\)で求めることができます。
ですが,そのやり方だと非常に計算が煩雑になる&計算の物理的意味がわけわからなくなるので,前節で取り上げた重心運動エネルギーと相対運動エネルギーに分けて考えてみましょう。\((2)\)もこの2種類に分割すれば,
とすることができます。こうすることで,先に取り上げた二種類に分割することの意味がスッキリするはずです。
ここで運動量保存則を思い出してみましょう。衝突や分裂において運動量の合計値が必ず保存するから,\[ m_1v_1 + m_2v_2 = m_1v’_1 + m_2v’_2\]が成立します。この全運動量は重心速度と比例するため,
全運動量保存 = 重心運動エネルギー保存
という関係が成立します。
まとめ
ここで大事なことは次の点です。
- 2物体のエネルギーは重心運動と相対運動に分けて考える
- 衝突前後で重心運動エネルギーは保存される
- ゆえにエネルギー変化は相対運動エネルギー変化のみ
- 相対速度は衝突前後で単に\(e\)倍
これだけおさえておけばややこしい問題でもスムーズに答えにたどり着けるはずです!
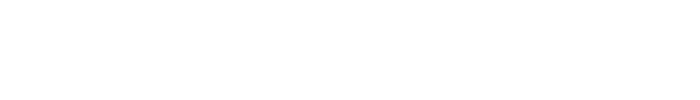
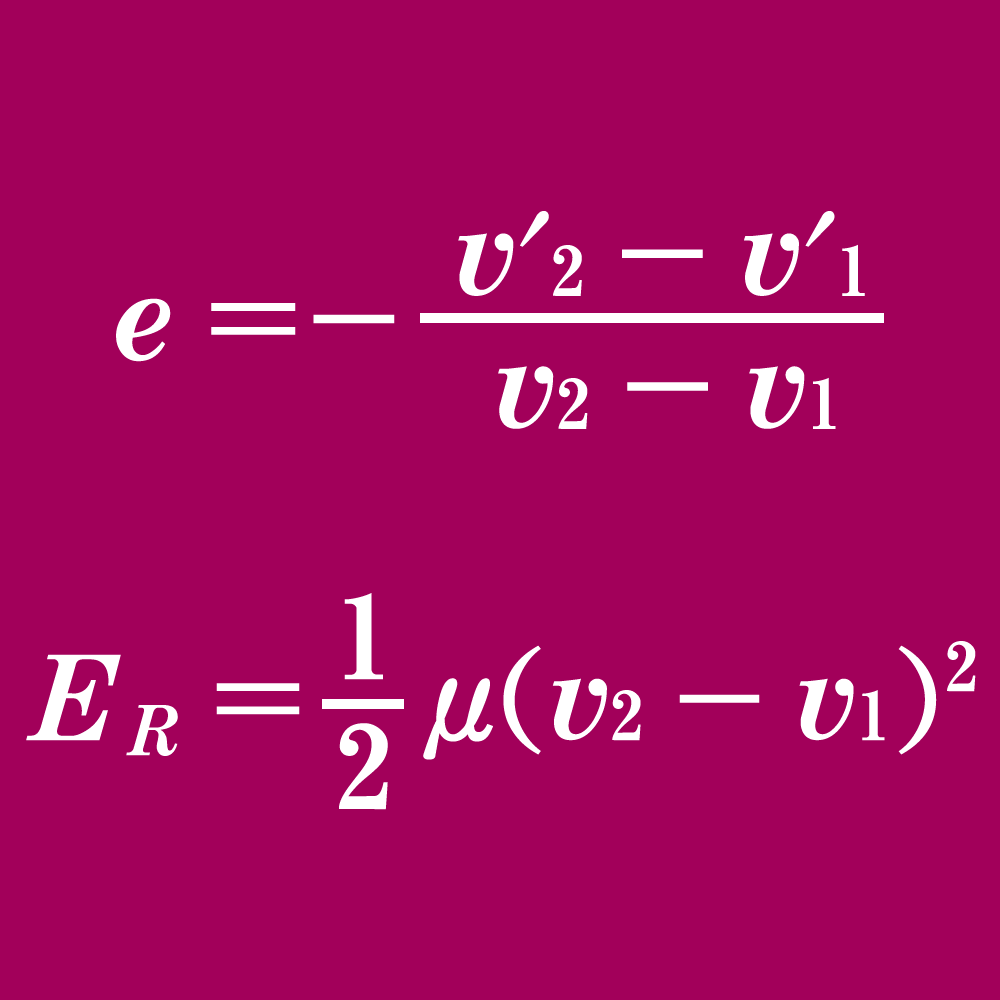
コメント
学校ではここまでエネルギーとの関係を教えてくれなかったので、非常に勉強になりました
ですが、エネルギーの減少量の最後の式はeではなく(1-e^2)です
copyソルさん
コメントありがとうございます。
ご指摘の通り誤りでしたので、修正いたしました。
これの速度はベクトルの時だけですか?スカラー量でも成り立ちますか?