大学の物理で出てくる応力という力。新しく出てきた上に,それがテンソルと言われてもピンとこないですが,図的に捉えるとしっくりくると思います。
応力とは何か
一言で言えば,応力とは面に働く力です。中学校までの理科でも圧力という物理量を習ったと思います。圧力とは単位面積あたりに働く力(多くは力の大きさを作用する面積で割って求めたと思います)であり,実はこの圧力も応力の1つです。
力の単位はN(ニュートン)で,面積の単位は平方メートルですから,応力の単位は圧力と同じPa(パスカル)となります。SI単位系であれば,1平方メートルあたりに働く力の大きさと考えれば良いですね。
ただしこれは厄介なことに,我々の住む3次元の世界では9つの成分をもつテンソルというもので定義されます。ここが非常にわかりづらく,多くの人が敬遠してしまうポイントなので丁寧に解説していきます。
まず高校物理でもやる「力」を思い出してみてください。力はベクトル量で3成分あると教わったはずです。デカルト座標では\(x, y, z\)軸方向の3成分と考えることができます。(極座標系ではまた別ですが)
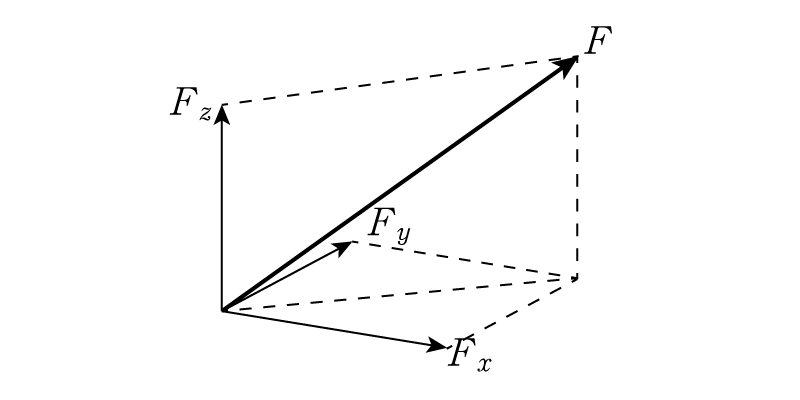
これを頭に留めながら,応力の成分も見ていきましょう。
応力には9つの成分がある
さていきなりエッセンスを書いてしまいましたが,力が3成分なのに対して,応力は9つの成分を持ちます。どういうことかというと,3方向の面に対して3方向の力がかかるので,3×3=9つの成分によって応力は定まります。図にするとこのようになります。
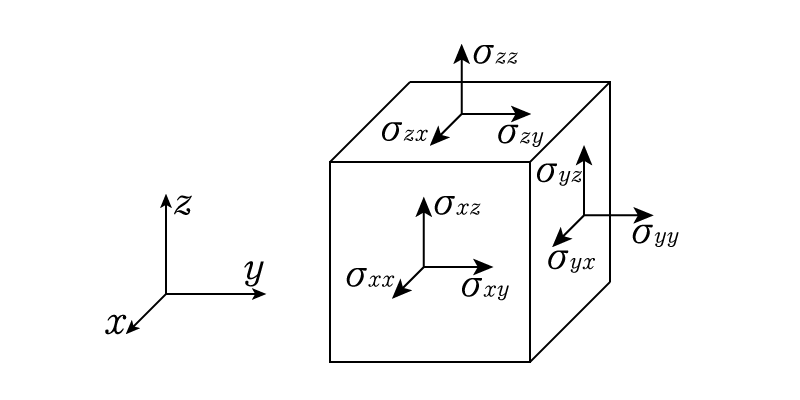
テンソルはギリシャ文字σ(シグマ/小文字)を用いて表すことが多いです。英語ではstressですから,その頭文字をギリシャ文字にしたんですね。
ポイントは行列と同じく,添え字が2つあるということです。それぞれが\(x,y,z\)になり得るので成分は9つあり,3×3行列で表現できます。\[ \sigma = \begin{pmatrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{pmatrix} \] ではそれぞれの添え字は何を表しているのでしょうか。
まず1つめは力が作用する面を表しています。例えば\( \sigma_{xx}, \sigma_{xy}, \sigma_{xz}\)の3つは1つめの添え字が\(x\)ですが,これは\(x\)軸の方向を向く面に作用していることを表しています。図を見るとわかりやすいですが,この3つが作用している面は手前を向いている面,つまり\(x\)軸方向を向いている(\(x\)軸に垂直な)面ですね。他の軸も同様に考えることがでいます。
次に2つめは力の向きを表しています。例えば\( \sigma_{zx}, \sigma_{zy}, \sigma_{zz}\)の3つは2つめの添え字が\(z\)ですが,図上で全て\(z\)軸方向を向いた矢印(力)として表されています。普通の力と異なり,力の方向が同じでも作用する面が異なると違う成分としてカウントされるのが応力の特徴です。
応力テンソルの対称性と主応力
さて,先ほどは応力を行列の形で表現しましたが,より一般化して応力は2階テンソルであると考えます。要は添え字2つを指定すれば値が定まるもの,ぐらいの理解で大丈夫です。
このテンソルは9つの成分を持ちますが,独立な成分は6つだけです。それはこれが対称テンソル(添え字を交換しても値が不変)だからで\[ \sigma_{xy} = \sigma_{yx}, \quad \sigma_{yz} = \sigma_{zy}, \quad \sigma_{zx} = \sigma_{xz} \]が成立します。この添え字がお互いに異なる成分(行列における非対角成分)をせん断応力と呼びます。
実はこのせん断応力はうまく応力テンソルを変形してやることで消すことができます。応力は(いわゆる普通の)力と同じく,座標系と無関係に存在するものですから,座標系ごとに成分は異なるはずです。例えば一番上の図で,\(\vec{F} = (F_x, F_y, F_z)\)と分けて考えましたが,それこそ\(\vec{F}\)の方向と\(x\)軸が一致するように座標系を取ってしまえば,\(x\)成分しか持たない力に見えたはずです。
応力でも同じことができます。適当な座標を取ってやることで,せん断応力をゼロにすることができます。数学的操作としては,応力テンソルを表す行列を対角化することに対応します。\[ \begin{pmatrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{pmatrix} \to \begin{pmatrix} \sigma’_{xx} & 0 & 0 \\ 0 & \sigma’_{yy} & 0 \\ 0 & 0 & \sigma’_{zz} \end{pmatrix} \]このように対角化して出てきた成分を主応力と呼びます。こうすることで応力場のエッセンスを捉えることができます。
偏差応力について
最後に偏差応力について紹介しておきます。応力\(\sigma\)に対してその偏差応力を\(\sigma_d\)と書くと,次のように定義されます。\[\sigma_d = \sigma+pI\]ここで\(I\)は単位行列で\[p=-\dfrac{\sigma_{xx}+\sigma_{yy}+\sigma_{zz}}{3}\]です。この\(p\)は静水圧と呼ばれ,応力の体格成分(垂直応力)の平均値です。この偏差応力は,応力に等方的でない成分が入っている場合ゼロでなくなります。逆にいうと,応力が完全に等方的なら偏差応力は存在しません。覚えておくといいですね。
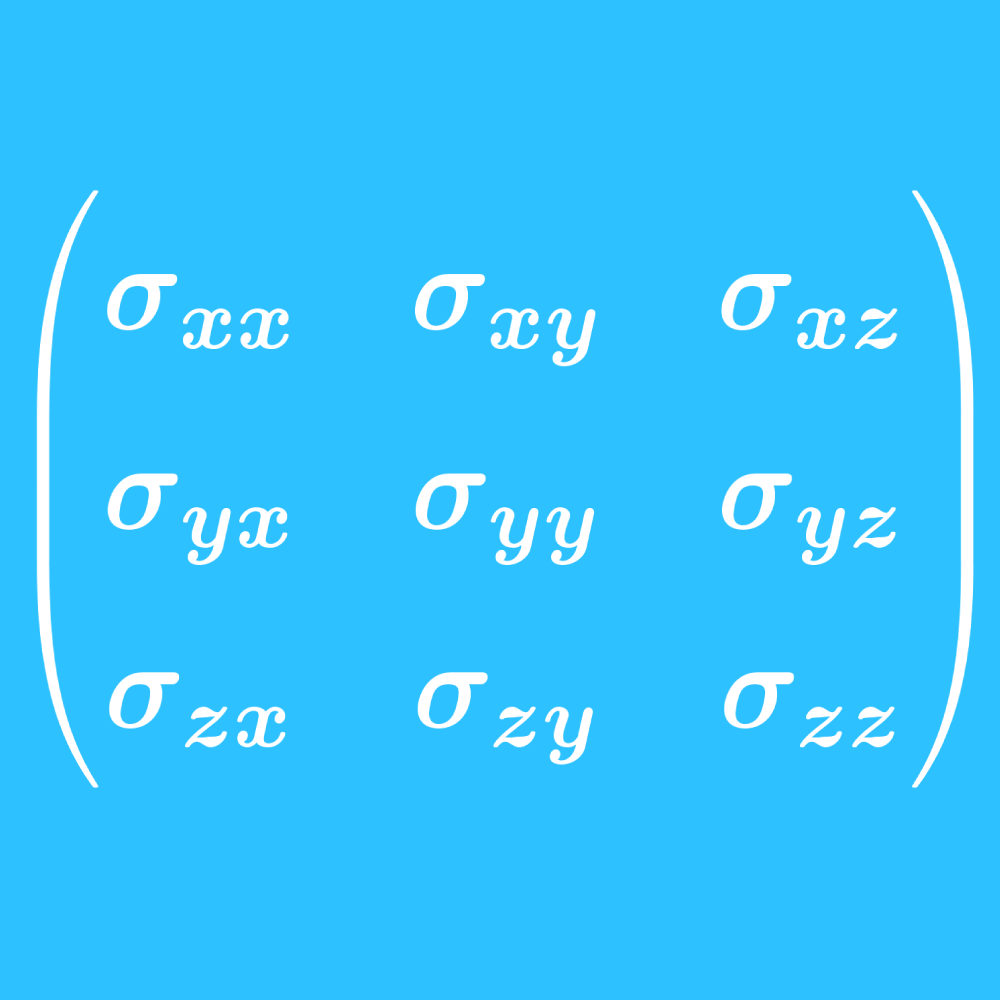
コメント