【解説】東京大学2019年度第2問

東京大学2019年度入試の物理第2問の解説ページです。問題のPDFファイルはこちらからダウンロードできます。なお，問題そのものの著作権は東京大学に帰属します。ご注意ください。

設問Ⅰ

抵抗値と静電容量を答えさせる問題ですが，これは教科書にも書いてあるレベルの話なので大丈夫でしょう。抵抗値は抵抗の長さに比例し，断面積に反比例してその比例係数が抵抗率だから，\[ R=\rho \dfrac{d}{S}\]で，静電容量は電場と電位の関係式から導出できて，次の通りです。\[ C=\varepsilon\dfrac{S}{d}\]

なお，この装置１つ１つは問題に書かれている通り，抵抗とコンデンサーを並列接続したものとみなせる，というところがポイントです。並列接続なので，この２素子の電圧は等しいはずです。

設問Ⅱ

上で考えた装置を\(N\)個直列に接続したものに，直流電源・抵抗・交流電源のいずれかを繋いで，その時の状態を問う問題です。簡略化した回路図を自分で書いて，どのように電流が流れているのかを落ち着いて考えれば十分答えにたどり着ける問題だと思います。

小問(1)

直流電圧に接続して十分に時間が経つと，コンデンサーへの蓄電が完了するため，コンデンサーには電流が流れなくなります。つまり，この場では抵抗のみに電流が流れます。１つあたり抵抗値\(R\)の抵抗を\(N\)個直列に繋いでいるから，その合成抵抗は\(NR\)です。

したがって，素子Ｘに流れる電流（\(I_1\)とおく）は，\[NRI_1 = V_0 \quad よって \quad I_1 = \dfrac{V_0}{NR}\]となります。すると，抵抗１つあたりの電圧は\[R\times\dfrac{V_0}{NR} = \dfrac{V_0}{N}\]となりますから，コンデンサーの電圧もこれに等しくなります。コンデンサーの電気量を\(Q_1\)と書けば，コンデンサーの基本式より，\[Q_1=\dfrac{CV_0}{N}\]と求められます。

小問(2)

スイッチを切り替えて抵抗に接続して電流が流れるのは，素子Ｘが\(V_0\)の電圧を持つ起電力のように働いたからです。また十分時間が経って電流が流れなくなったのは，素子Ｘが蓄えていた静電エネルギーが，抵抗でのジュール熱として発散していったからです。

素子Ｘが蓄えていたエネルギー\(E_1\)は\[E_1=\dfrac{C{V_0}^2}{2N}\]でした。これが抵抗で発散したわけですが，ジュール熱が\[VI=RI^2=\dfrac{V^2}{R}\]のいずれの形でも書けることを考えると，外部抵抗\(R_0\)と素子の抵抗\(NR\)は電圧が等しいので一番右の形を使って考えます。電圧が等しければ，ジュール熱は抵抗に反比例しますから，この\(E_1\)は素子Ｘと外部抵抗で\(R_0:NR\)に分配され発散したと考えられます。したがって，外部抵抗で発散した分は次のように計算できます。\[E_1 \cdot \dfrac{NR}{NR+R_0} = \dfrac{R}{2(NR+R_0)}C{V_0}^2\]この式から，\(N\)を増やしていくと分母が大きくなり，外部抵抗で発生するジュール熱は単調に減少することがわかります。

小問(3)

次にスイッチを交流電源に接続しますが，接続する直前は電流も流れていなければコンデンサーの電気量もありません。本当の回路は左図のようになっていますが，超簡略化して書くと右図のようになります。

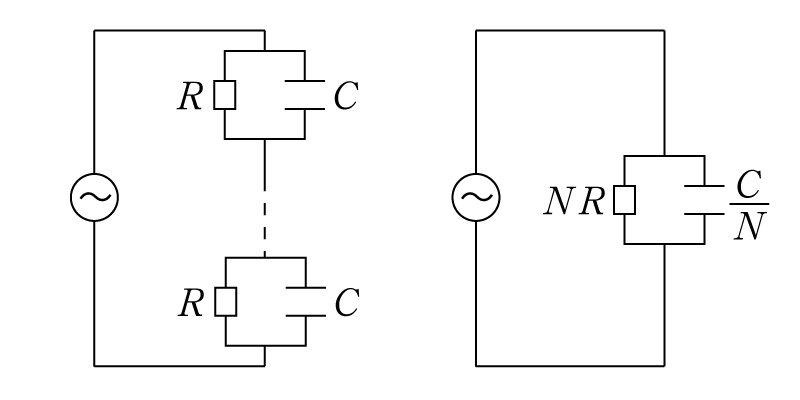
ごちゃごちゃしてるまま考えると死ぬので，簡略化して考えましょう。抵抗\(NR\)とコンデンサー\(C/N\)が交流電源に並列接続されているだけです。抵抗に流れる電流\(I_R\)は，オームの法則から，\[I_R=\dfrac{V_1}{NR}\sin\omega t\]となります。またコンデンサーの電気量を\(Q_2\)と書くと，コンデンサーの基本式から，\[Q_2=\dfrac{CV_1}{N}\sin\omega t\]となりますが，コンデンサーの電流\(I_C\)は電気量の時間変化率（微分）に等しいから，\[I_C=\dfrac{dQ_2}{dt}=\dfrac{\omega CV_1}{N}\cos\omega t\]となります。求めるべき電流はこの合計だから，答えは次のようにかけます。\[\dfrac{V_1}{NR}\sin\omega t + \dfrac{\omega CV_1}{N}\cos\omega t\]

微分を使わない方針ならば，コンデンサーを流れる電流は電圧に対して\(\pi/2\)だけ位相が進むこと，さらにコンデンサーのリアクタンスが\(\dfrac{N}{\omega C}\)であることを用いれば，\(I_C\)を求めることができます。

設問Ⅲ

誘導に従っていけば答えにたどり着ける問題だと思います。Ｌ〜Ｋ間に電流が流れなくなったということは，ＬとKの電位は等しいということになります。またその区間に電流が流れないことにより，\(R_1\)を流れる電流と\(2R_1\)を流れる電流は等しくなるから，それを\(I_2\)とおくと，\[I_2=\dfrac{V_1}{3R_1}\sin\omega t\]となります。従って，K〜Ｍ間の電圧［ア］は\[2R_1I_2=\dfrac{2V_1}{3}\sin \omega t\]です。この電圧はＬ〜Ｍ間の電圧でもあるから，\(R_2\)を流れる電流を\(I_3\)，コンデンサー\(C_0\)の電気量を\(Q_3\)と書くと，\[R_2I_3+\dfrac{Q_3}{C_0}=\dfrac{2V_1}{3}\sin \omega t\]ですが，コンデンサーの容量は与えられているので代入して，さらに全体を微分します。\(Q_3\)の微分が\(I_3\)であることに注意すると，\[R_2\dfrac{dI_3}{dt}+\omega R_2I_3=\dfrac{2\omega V_1}{3}\cos \omega t\]という微分方程式を得ます。\(I_3\)の形は誘導で与えられていますから，［イ］と［ウ］をそれぞれ\(A,B\) とおいて，この微分方程式に代入します。

\[\omega R_2(A\cos\omega t-B\sin\omega t) + \omega R_2(A\sin\omega t+B\cos\omega t) = \dfrac{2\omega V_1}{3}\cos \omega t\]

となりますから，sinとcosで左辺を整理して，\[(A+B)\cos\omega t+(A-B)\sin\omega t=\dfrac{2V_1}{3R_2}\cos\omega t\]となるから，係数を比較してあげて，\[A=B=\dfrac{V_1}{3R_2}\]となります。なかなか面倒ですね。

さて，Ｊ〜Ｋ間の電圧［エ］は残りの\[\dfrac{V_1}{3}\sin\omega t\]であることはすぐにわかります。素子Ｘは抵抗\(NR\)とコンデンサー\(N/C\)の並列接続ですから，抵抗もコンデンサーも電圧は［エ］に等しいはずです。つまり設問Ⅱ(3)と同様に考えて，抵抗を流れる電流は\[\dfrac{V_1}{3NR}\sin\omega t\]で，コンデンサーを流れる電流は\[\dfrac{\omega CV_1}{3N}\cos\omega t\]ですから，この２つよりＪ〜Ｌ間を流れる電流［オ］［カ］は\[\dfrac{V_1}{3NR}\sin\omega t+\dfrac{\omega CV_1}{3N}\cos\omega t\]となります。

最後に，Ｊ〜Ｌ間を流れる電流とＬ〜Ｍ間を流れる電流は一致しなければならないから，\begin{align} &\dfrac{V_1}{3R_2}\sin\omega t+\dfrac{V_1}{3R_2}\cos\omega t \\ &= \dfrac{V_1}{3NR}\sin\omega t+\dfrac{\omega CV_1}{3N}\cos\omega t \end{align}が成立します。係数が一致する条件として次を得ます。\[R=\dfrac{R_2}{N}, \quad C=\dfrac{N}{\omega R_2}\]そして，設問Ⅰで求めた形を代入して，\[\rho\dfrac{d}{S}=\dfrac{R_2}{N}, \quad \varepsilon\dfrac{S}{d}=\dfrac{N}{\omega R_2}\]となるから，最終的な答え（抵抗率と誘電率）は次のようになります。\[\rho=\dfrac{SR_2}{dN}, \quad \varepsilon=\dfrac{dN}{\omega SR_2}\]