力学の基本となる運動の記述において重要な等加速度運動。公式の丸暗記ではなく,速度と時間のグラフを用いて考えることで,理解が深まります。
等加速度運動の3公式
まず,等加速度運動とは読んで字のごとく各方向で加速度が一定である運動のことです。速度と加速度,また運動を記述するにあたり必要な時間の導入についてはこちらのページを参考にしてください。
教科書にも出てくる重要な公式は次の通りです。
(1) \quad & v = v_0 + at \\
(2) \quad & x = v_0 t + \dfrac{1}{2}at^2 \\
(3) \quad & v^2 \, – \, {v_0}^2 = 2ax
\end{align}
速度の公式
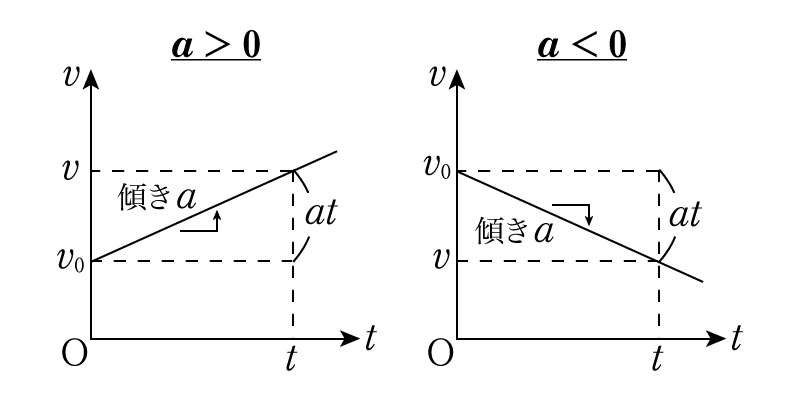
この式は初速\(v_0\)でスタートした物体が加速度\(a\)で運動しているときの,時刻\(t\)での速度\(v\)を表しています。加速度が速度の時間変化率であるということに気づいていればすんなり入ると思いますが,式の形だけを見ると\(v\)は\(t\)の1次関数となっています。つまり,グラフは次のようになるはずです。
変位の公式
この式は初速\(v_0\)でスタートした物体が加速度\(a\)で運動しているときの,時刻\(t\)での変位\(x\)を表しています。変位ですから\(t=0\)での位置を基準としてどれだけ位置が移動したかを計算できるのですが,こちらのページでも言及したように,正の向きをきちんと定める必要があります。つまり,
加速度\(a\),初速\(v_0\),変位\(x\)をはかる向きは統一する必要がある
ということです。この式も\(v-t\)グラフを用いることで簡単に理解できます。ここでは加速度が正の場合のみ扱いますが,負の場合も上の速度の公式同様ですので,まったく同じです。

さて非常に大事なことですが,速度のグラフが囲む部分の面積が変位に対応するのでした。ですから,上のように速度が時間の1次関数(グラフは直線)の場合,それが囲む部分は台形になります。上の図ではその台形を下側の長方形と上側の三角形に分割して考えました。このとき,
- 下は底辺\(t\),高さ\(v_0\)の長方形
- 上は底辺\(t\),高さ\(at\)の三角形
になりますから,それぞれの面積を計算して足すことによって変位が次のように求まります。\[ x(t) = v_0 t + \dfrac{1}{2}at^2 \]速度のときに比べて文字の数が多くて少し紛らわしいですが,このように図形的イメージを持つことで間違えにくくなります。例えば初速がゼロでスタートしたなら,変位は\(at^2/2\)と簡潔に書けることもこの式からわかりますね。
速度の二乗の変化の式
さて最後は速度の二乗がどれだけ変化するかを表した式です。実はこの式(3)は,上の二つの式(1)と(2)を連立させて\(t\)を消去すれば求めることができます。つまり(1)から,\[ v = v_0 + at \quad ゆえに \quad t = \dfrac{v-v_0}{a} \]となり,これを(2)に代入します。
\begin{align}
x &= v_0 \dfrac{v-v_0}{a} + \dfrac{1}{2}a \left( \dfrac{v-v_0}{a} \right)^2 \\[1mm]
&= \dfrac{vv_0-{v_0}^2}{a} + \dfrac{v^2 – 2vv_0 + {v_0}^2}{2a} = \dfrac{v^2 – {v_0}^2}{2a}
\end{align}
となりますから,最後に両辺\(2a\)倍して\[ v^2 – {v_0}^2 = 2ax \]という公式を得ます。なんでこんなことまでしてこの公式を求めて使っていくのかというと,時間\(t\)が式にいないことが嬉しいのです。この式は物体がどの位の時間をかけて移動したかがわからなくても,加速度と変位がわかっていれば速度の二乗変化がわかる優れモノなのです。
具体例で使い分けをマスター
多くの高校生の悩みはこの式を,どういう場合でいつ使うのかで悩んでいると思いますので,具体例を挙げて少し説明しておきます。
問.初速\(8 \,\mathrm{m/s}\)で打ち出した球が,初速と逆向きの加速度\(2 \,\mathrm{m/s^2}\)で運動した。\(5 \,\mathrm{s}\)後の変位(初速方向を正)を求めよ。
答.これは初速,加速度,時間が与えられて変位を聞かれているので(2)を使います。ただし,加速度は初速や変位に対して逆向きですから負の数として取り扱います。したがって計算式は次のようになります。\[ x = 8 \cdot 5 + \dfrac{1}{2} \cdot (-2) \cdot 5^2 = 15 \,\mathrm{m}\]
別の例もやってみます。
問.ある物体がとある初速で打ち出されて,初速の向きに加速度\(4 \, \mathrm{m/s^2}\)で運動した。\(6 \,\mathrm{s}\)後の速度が\(30 \,\mathrm{m/s}\)のとき,初速はいくらか。
答.少し曲がった問われ方をしていますが,本質は変わりません。初速が知りたくて,与えられた条件は\(6 \,\mathrm{s}\)後の速度です。ですから,速度の公式を使えばいいですね。初速を\(v_0\)とすると,\[ 30 = v_0 + 4\cdot 6\]となりますから,\(v_0 = 6 \,\mathrm{m/s}\)と求まります。
もう一つ考えてみましょう。
問.小球が初速\( 3 \,\mathrm{m/s}\)で動き始め,加速度は初速の向きに\(2 \,\mathrm{m/s^2}\)であった。小球の変位が\(4 \,\mathrm{m}\)となったときの速度はいくらか。
答.問題文中に時間の情報がありませんから,一発で(3)の式を使うことがわかります。求める速度を\(v\)とすると,\[ v^2 – 3^2 = 2\cdot 2\cdot 4 \quad ゆえに \quad v^2=16\]と求められます。さてここで一つ引っかかるのが,この式からは数学的には\(v=\pm 4\,\mathrm{m/s}\)と2つの答えが出てきます。もちろん,初速が初速\( 3 \,\mathrm{m/s}\)で,初速の向きに加速されてますから答えはプラスの\(v=4\,\mathrm{m/s}\)だけですが,ではマイナスの答えは何を意味するのでしょうか。それは(1)の式にこのマイナスの答えを入れてみるとわかります。実際にいれてみると,\[ -4 = 3 + 2\cdot t \]となりますが,これを解くと\( t = -3.5 \,\mathrm{s}\)となってしまいます。初速が出る\(t=0\)以前のことは今関係ないですから,この解は除外しないといけない,ということになります。
ここまでが実際に等加速度運動の公式を適用する例でしたが,単に速度や変位を聞かれるだけでなく,初速等も問われる対象になりうることがわかったと思います。大事なのは,問題で何を聞かれて何を問われているのかまず整理することです。公式をしっかり理解したうえで,それができればどの式を使うか迷うことはなくなると思います。
また最後の例であったように(3)の式を使う際は,時間の項が式から消えているせいで,物理的にはあり得ない答えも数学的にははじき出される可能性があります。盲目的に式に従うのではなく,実際の現象を意識しながら使うようにしましょう。
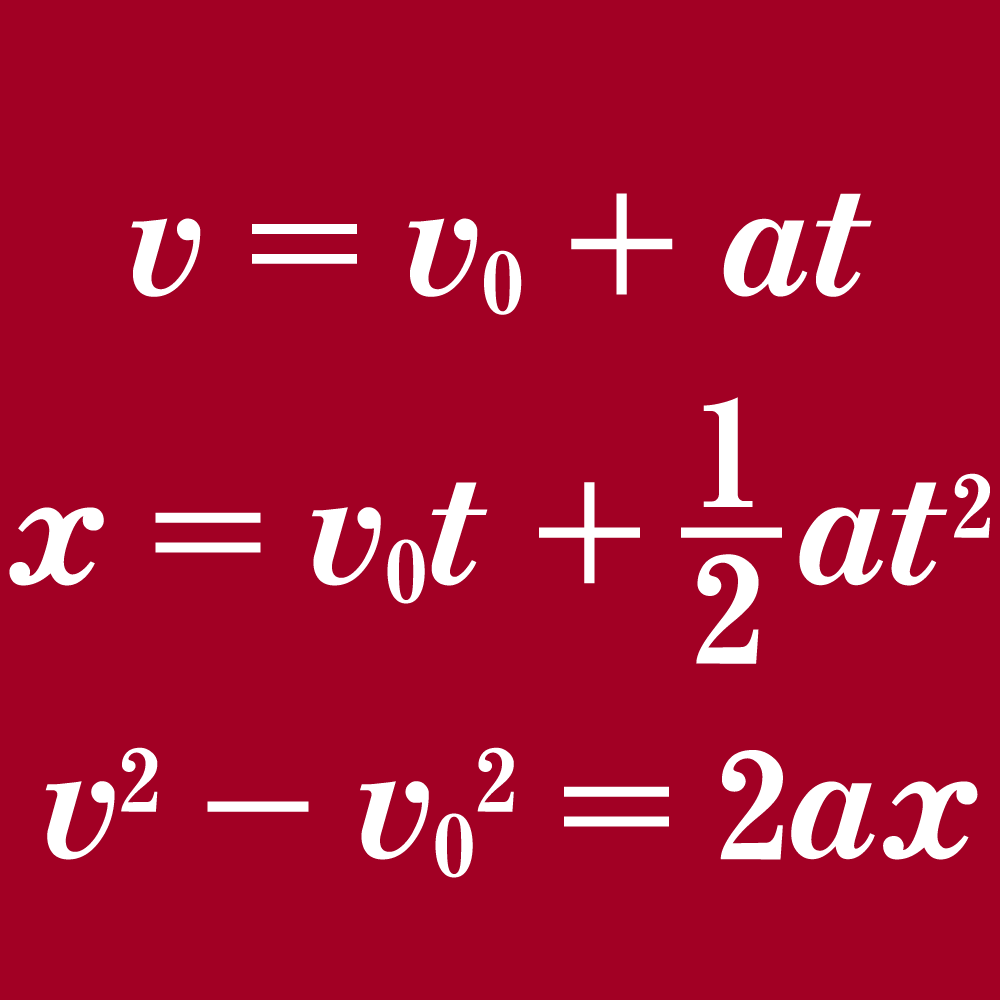
コメント