物体の回転のしづらさを表す慣性モーメント。大きさを持つ剛体では積分の形で定義されるため,煩雑になりがちですが,代表的な形状における計算法やその値は覚えておく価値があると思います。
大きさを持つ剛体の慣性モーメント
回転軸から距離\(r\)だけ離れた質量\(m\)の質点がもつ慣性モーメントは\(mr^2\)と書かれました。これについてはこちらのページも参考にしてください。大きさを持つ剛体では,この質点を無数個集めたものとして考えることができます。つまり,剛体中の微小体積\(dv\)の部分がもつ慣性モーメントを剛体の領域で積分することで全体の慣性モーメントを計算することができます。
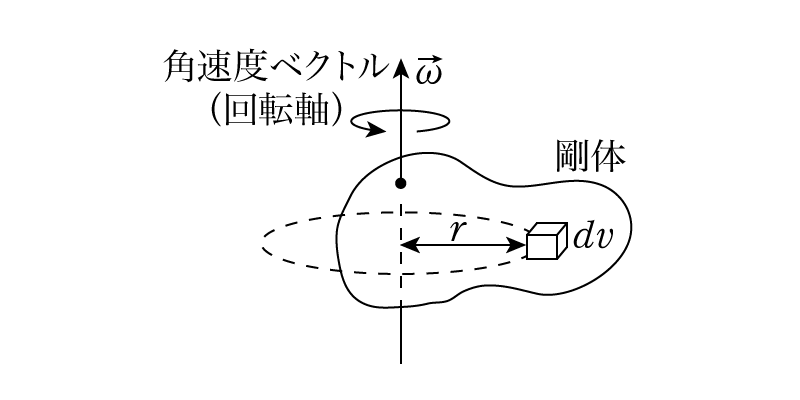
もちろん,回転軸をどこにするかによって距離\(r\)は異なってきますから注意が必要です。また微小部分の質量は,その物体の密度\(\rho\)を用いて\(m=\rho dv\)と書けます。以下ではこの密度は至る所一定であるという仮定に基づいて計算をしていきます。ゆえに,剛体が占める領域を\(V\)と書くとその慣性モーメント\(I\)は\[ I = \int_V \rho r^2 dv\]と書くことができます。これを用いて,種々の形状における慣性モーメントを計算していきましょう。
なお,次章以降では多重積分をしていきますが,必要に応じて円筒座標や極座標での積分をするために変数変換をします。その辺を先に復習しておきたい場合は以下のページを読んでからの方が飲み込みやすいと思います。
円柱の慣性モーメント
底面の半径が\(R\),高さが\(h\)の円柱を考えます。積分計算が実行できるように円柱の重心を\(xyz\)空間の原点に置き,底面を\(xy\)平面と平行にします。図にすると下のようになります。
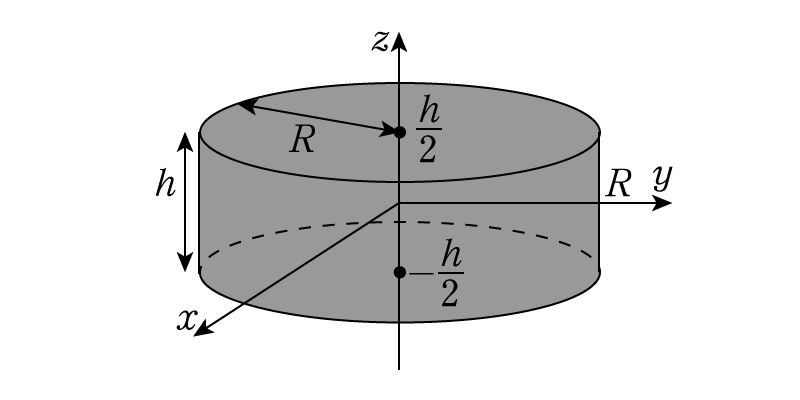
一応数学的に不等式で表記してみると\[0 \leq x^2+y^2 \leq R^2, \quad -\dfrac{h}{2} \leq z \leq \dfrac{h}{2}\]です。まずは\(z\)軸まわりの慣性モーメント\(I_z\)から考えます。定義から\begin{align} I_z &= \int_{-h/2}^{h/2}dz \int_{0\leq x^2+y^2 \leq R^2} \rho (x^2+y^2) dxdy \\ &= h\int_{0\leq x^2+y^2 \leq R^2} \rho (x^2+y^2) dxdy\end{align}と書くことができます。\(z\)方向には一様なので,高さ倍されるだけですが\(xy\)平面に関する積分は極座標を用いることで簡素化できます。積分の微小面素は\((x,y) \to (r,\theta)\)の変換で,\[ dxdy = rdrd\theta\]と変換されますから,次のように積分は簡単になります。\[I_z = \int_0^{2\pi}d\theta \int_0^R \rho r^3 dr = \dfrac{\rho\pi R^4h}{2}\]これで求められたのですが,実用上は物体の密度より物体の質量の方がはるかに簡単にわかるので,物体の質量\(M\)を用いて表記しておいたほうが便利です。また質量を用いることにより,無限に薄い円板に対しても同じ表式が使えるようになります。質量は密度と体積の積だから\[ M = \rho \cdot \pi R^2 h\]です。これを代入することによって円柱の\(z\)軸まわりの慣性モーメントは\[ I_z = \dfrac{MR^2}{2}\]と計算できます。
次に\(x\)軸,\(y\)軸まわりの回転を考えますが,形状の対称性からそれぞれの軸まわりの回転の仕方は全く同じですから,慣性モーメントも等しく\(I_x = I_y\)となります。\(I_x\)の方だけ計算することにすると,今回も(x,y\)方向の積分は極座標に変換して,\begin{align} I_x &= \int_{-h/2}^{h/2} \int_{0\leq x^2+y^2 \leq R^2} \rho (y^2+z^2) dxdydz \\ &= \rho \int_{-h/2}^{h/2}dz \int_0^R rdr \int_0^{2\pi}d\theta (r^2\sin^2\theta+z^2) \\ &= \rho \int_0^R rdr \int_0^{2\pi}d\theta \left(hr^2\sin^2\theta + \dfrac{h^3}{12} \right) \\ &= \rho \left( \int_0^R \int_0^{2\pi} hr^3\sin^2\theta drd\theta + \dfrac{\pi R^2 h^3}{12} \right)\\ &= \rho \left(\dfrac{\pi R^4h}{4}+ \dfrac{\pi R^2 h^3}{12} \right) \\ &= \rho \pi R^2 h\left(\dfrac{R^2}{4}+ \dfrac{h^2}{12} \right) = M\left(\dfrac{R^2}{4}+ \dfrac{h^2}{12} \right)\end{align}と求まります。\(z\)方向の積分を最初にやり,その後\(r,\theta\)方向に積分をしています。最後は例によって物体の質量を用いて表記しています。これは覚えるようなものでもない気がするので,このような計算をすれば出るのだというのを頭に入れておくようにしましょう。
球体の慣性モーメント
次に半径\(R\)の球体の慣性モーメントを考えます。例によってその重心を\(xyz\)空間の中心に置くと,この球体が占める領域\(V\)は\[ V: \ 0 \leq x^2+y^2+z^2 \leq R^2\]と表現できます。また明らかに球対称なのでどの軸を中心に回しても慣性モーメントは等しくなることがわかります。つまり,\[ I = I_x = I_y = I_z\]とおくことができるのですが,円柱の時のように真面目に積分するより便利でよく用いられる方法が2つあるので,そちらを紹介していきます。
対称性を利用する方法
全ての軸まわりの慣性モーメントが等しいので,\[ I = \dfrac{I_x + I_y + I_z}{3}\]となります。これに軸まわりのモーメントの表式を代入すると,\begin{align} I &= \dfrac{1}{3} \left\{ \int_V \right. \rho(y^2+z^2)dxdydz \\ &\quad\quad + \int_V \rho(z^2+x^2)dxdydz \\ &\quad\quad + \left. \int_V \rho(x^2+y^2)dxdydz \right\} \\[1mm] &= \dfrac{2}{3} \rho \int_V (x^2+y^2+z^2) dxdydz\end{align}です。 ここで3次元の極座標変換\((x,y,z)\to(r,\theta,\phi)\)を行います。この変換では微小体積要素は\[ dxdydz = r^2\sin\theta drd\theta d\phi\]と変換できるから,この慣性モーメントは\begin{align} I &= \dfrac{2}{3}\rho \int_0^R r^4 dr \int_0^{2\pi}d\phi \int_0^{\pi}\sin\theta \, d\theta \\ &= \dfrac{8}{15}\rho\pi R^4\end{align}と求めることができます。また,球体の質量\(M\)はその密度を用いて\[ M = \rho \cdot \dfrac{4}{3}\pi R^3\]と書けることを用いれば,慣性モーメントは\[ I = \dfrac{2}{5}MR^2\]と書くことができます。
円柱のモーメントを利用する方法
別のやり方に,上で求めた円柱(円板)の慣性モーメントを使う計算方法があります。これは積分の基本的なアイデアと非常によく似ていて,球体は様々な半径をもつ薄い円板の集合体である,という考えに基づいています。 例えば下の図のように,\(z\)軸方向に薄くスライスすると,厚さ\(dz\)の円板を\(-R\leq z\leq R\)で集めたものが球であると考えることができます。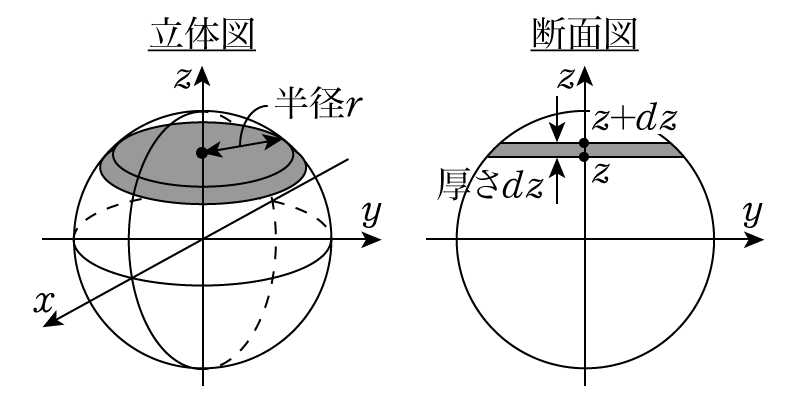
また三平方の定理から位置\(z\)における円板の半径\(r\)は\[ r=\sqrt{R^2-z^2}\]であるとわかります。したがって上で求めた円板の慣性モーメントの式を使えば,位置\(z\)で厚さ\(dz\)の円板のモーメント\(dI\)は\[ dI = \dfrac{\rho}{2}\pi (R^2-z^2)^2 dz\] です。これを\(-R\leq z\leq R\)で積分すれば良いから,慣性モーメントは\begin{align} I &= \int_{-R}^R \dfrac{\rho}{2}\pi (R^2-z^2)^2 dz \\ &= \dfrac{\rho}{2}\pi \int_{-R}^R (z^4 – 2R^2 z^2 + R^4)dz \\ &=\dfrac{8}{15}\rho\pi R^4 \end{align}と求められます。もちろん先ほどの対称性を利用した解法の結果と同じになりますね。
平行軸の定理
さて,これまでの解説では回転軸が物体の重心を通るような例ばかり取り扱ってきましたが,実際には回転中心は物体の重心でなくとも,物体の外部であっても良いです。そのような場合の慣性モーメントは回転半径\(r\)が変わるために変化してしまいますが,平行軸の定理と呼ばれるものを使うことで容易に計算できます。
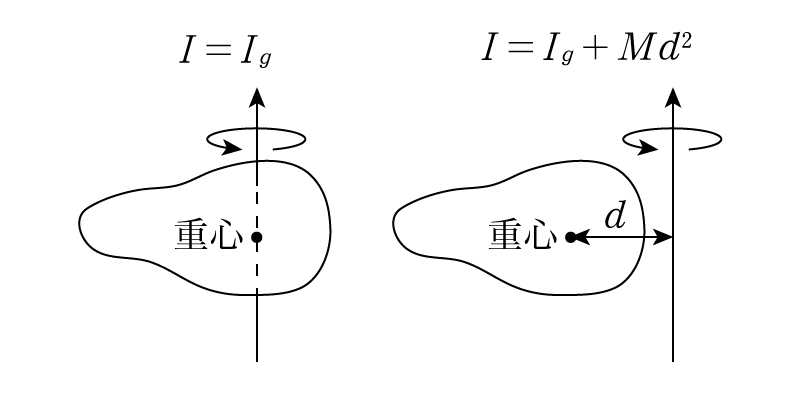
平行軸の定理
質量\(M\)の物体の重心を通る回転軸まわりの慣性モーメントが\(I_g\)である時,重心から\(d\)離れたところにある軸まわりの慣性モーメントは\(I_g+Md^2\)と表される。
最後に少し厳密な議論
ここまで慣性モーメントは3軸に対して求めてきましたが,より厳密には慣性モーメントは\(3\times 3\)行列で表されるテンソルです。成分をあらわに書くと,\[ I = \begin{pmatrix} I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zy} & I_{zz} \end{pmatrix} \]となり,今まで使ってきた\(I_x, I_y, I_z\)はこの行列の対角成分にすぎません。ではこの非対角成分は何なのかというと,回転軸がきちんとした方向を向いていない場合出てくる項です。すごく抽象的に表現してしまいましたが,3つの互いに直交する回転軸をそれぞれの物体に対して適切に取ることによってこの非対角成分は無くなるということです。球体はどの方向に回しても同じですが,例えば円柱を下の図のように回すとどうなるでしょうか。
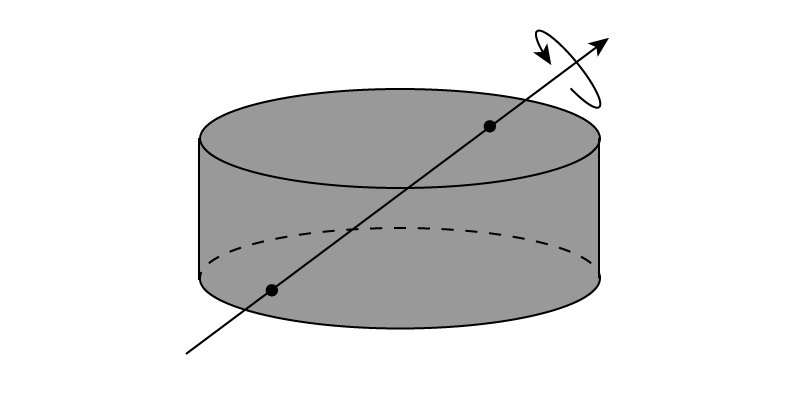
かなりめちゃくちゃな回り方をするのは想像できると思います。このような場合非対角成分が出てきてしまいますが,回転軸を適当に回転させることによって,先ほど計算したような綺麗な値が対角成分として出てきます。慣性モーメント行列の対角化をするために回転行列をかけるという数学的操作が,回転軸を適切に取るという物理的操作に対応します。まず一般の慣性モーメント行列の成分を全て求めるようなことはないと思いますが,考え方として頭の片隅に入れておくとお得だと思います。

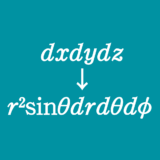
コメント