実生活に結びついていて,かなり身近に感じることも多い摩擦力。以下では物理学における摩擦力の由来と性質についてまとめました。特に高校レベルで出てくる2種類の摩擦力について区別できるようにしましょう。
摩擦力が生じる原因
まずはそもそもどのようにして摩擦力が生じるのかについて説明します。物体同士が触れ合っているとき,よく図では左のように書かれていますが,実際にその接触面を拡大してみると右のように非常にザラザラしていることがわかります。
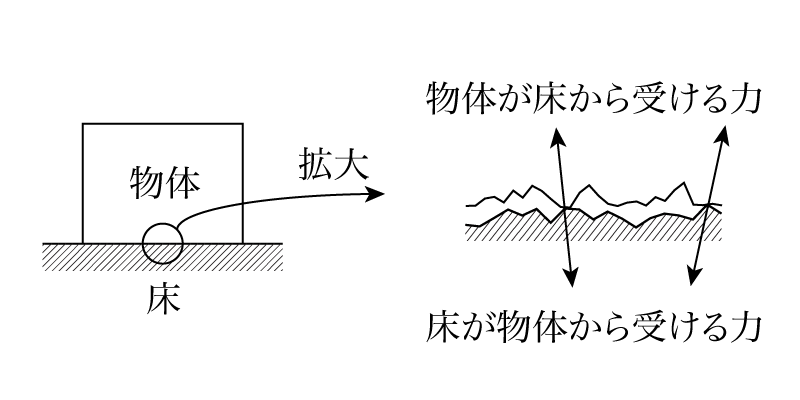
目で見たり手で触ったりした際にどんなに滑らかであると思えるような面も必ずこのような凹凸を持ちます。ゆえに物体が床の上に置かれているなどの物体が接触している状況においては,面と面が接しているように見えて実は物体同士が本当に接触している部分は極めて少ないと考えられています。
また原理的には物体が床から受ける力はそのような接触点での力を全て集めたものということができますが,接触点を1つ1つ数え上げて力を合算するのはあまりに非現実的です。したがって,次の図のようにまるっとまとめて(巨視的に)考えることにします。
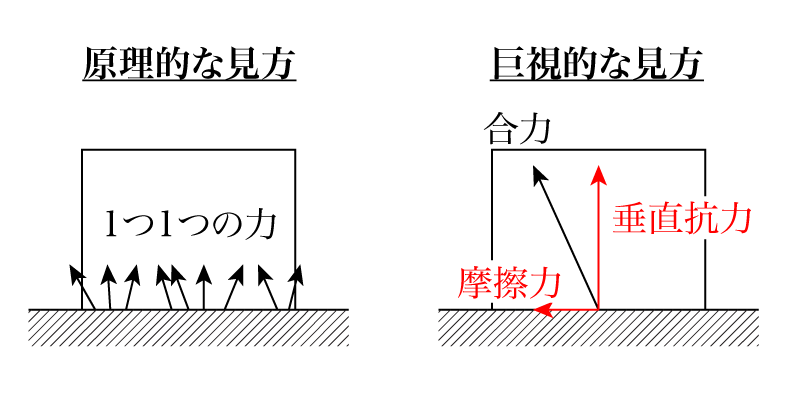
上の図でわかる通り,物理で用いられる垂直抗力と摩擦力は次のように決められます。
- 垂直抗力…相手方の物体から受ける抗力の鉛直成分
- 摩擦力…相手方の物体から受ける抗力の水平成分
つまり簡単にいえば,垂直抗力や摩擦力という「力」があるというよりかは,相手の物体から受ける力「抗力」の鉛直・水平成分のことをそれぞれ指しているにすぎません。
どのような場合にどのような摩擦力が働くのかについては次章以降で説明しますが,一般に物体が床などから受ける抗力は垂直とは限らないということに注意してください。
静止摩擦力
まず1つ目の摩擦力は静止摩擦力です。これは読んで字のごとく,物体が静止している際に働く摩擦力のことです。例えば上の例と同じように,ざらざらした床の上に物体が置かれている状況を考えてみましょう。もし外部から何も力を加えていないのであれば,静止摩擦力は存在しません。なぜならもし存在して上図右のように物体が斜めの抗力を受けていた場合,横方向に動き出してしまうはずですが,そんなこと起きたら怖いですよね。
ではどのような時に静止摩擦力は生じるかというと,物体が力を受けているのに動いていない時です。下の図を見てみてください。
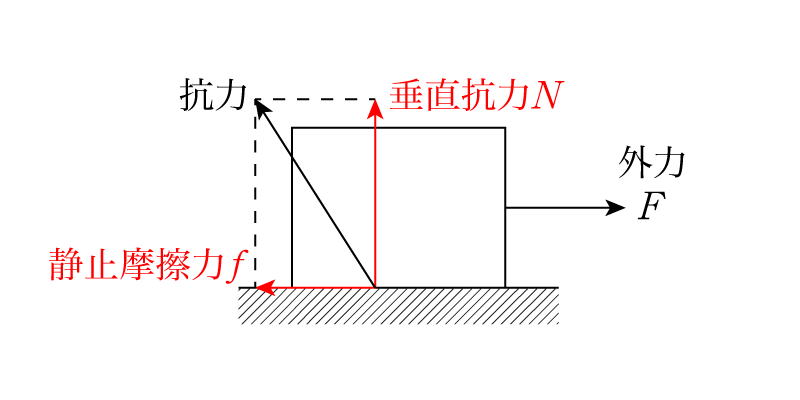
この場合,物体は右側に\(F\)という力で引っ張られていても静止しています。これは物体が動かないように,床が物体に対して静止摩擦力を外力と反対向きに加えているからです。つまり静止摩擦力は次のような性質を持ちます。
- 大きさは外力と等しい
- 向きは外力と反対
したがって数学的に記述するなら,力のつり合いから\(f=F\)とできます。しかし本当にこれは常に成り立つでしょうか。少し想像してみればわかりますがどんなに摩擦力があっても,相当に大きな力で引けばどんな物も動き出します。ゆえにこの静止摩擦力は最大値を持つはずで,最大となる時の摩擦力を特に最大静止摩擦力と呼びます。
最大静止摩擦力は,垂直抗力\(N\)の何倍か,という形で表されます。その係数を\(\mu\)と書き,最大静止摩擦係数と呼びます。したがって,静止摩擦力\(f\)は\(0 \leq f \leq \mu N\)の範囲を動くこととなります。この\(\mu\)は2つの物体のペアによって決まる定数で,実験的に調べることでわかるため,問題では与えられていることがほとんどです。
ここまでの話をグラフにまとめると,このようになります。
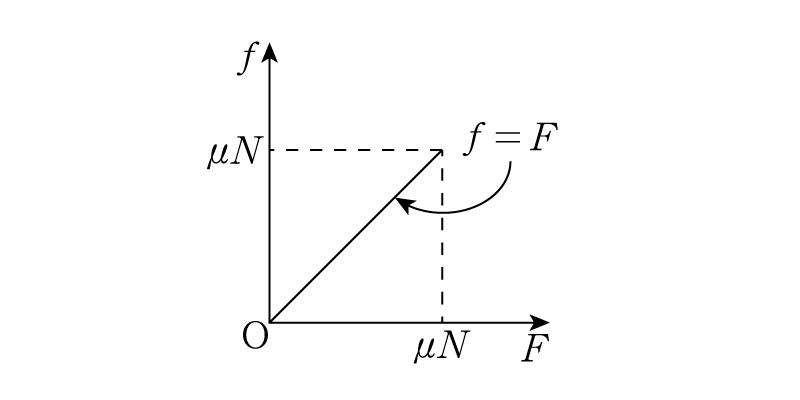
外力\(F\)が増えるにつれて,摩擦力\(f\)も増えていきますが,その上限は\(\mu N\)で抑えられます。では外力がそれより大きくなった時,物体が動き出しますがどのような摩擦力になるでしょうか。
動摩擦力
物体が動き出した後の摩擦力を動摩擦力と呼びます。これも最大静止摩擦力と同様に,垂直抗力\(N\)の何倍かで表して,その定数\(\mu’\)を動摩擦係数と呼びます。その性質は次の通りです。
- 大きさは外力に関わらず一定の\(\mu’ N\)
- 向きは物体が動く方向の反対
静止摩擦力との一番の違いは,外力がどんな値だろうと動いている限り,その大きさは一定であるということです。また動摩擦係数と静止摩擦係数の関係ですが,
動摩擦係数 < 最大静止摩擦係数
が必ず成立します。したがって\(f\)と\(F\)の関係を表すグラフは,静止時と合わせて次のようにかけます。
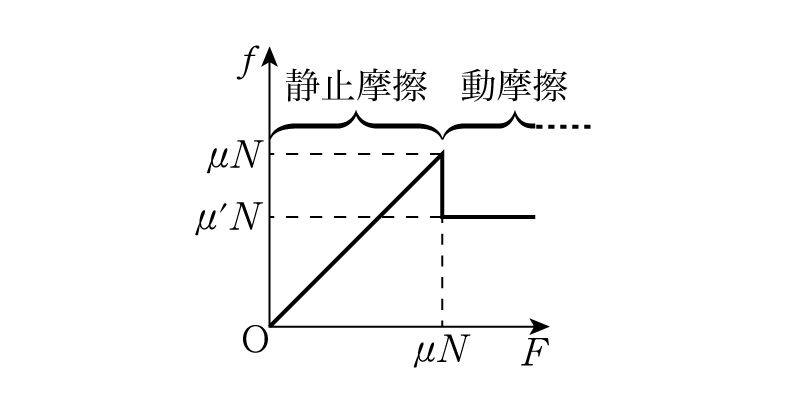
言い換えれば,動き出すまでに必要な力(最大静止摩擦力:\(\mu N\))は動き出してから必要な力(動摩擦力:\(\mu’ N\))より大きいということもできます。
重い物体が動きにくい理由
ここで日常的な話題を考えてみましょう。冷蔵庫や車といった非常に重い物体は,それに紐をくくりつけて引っ張っても,ちょっとやそっとじゃ動かないですよね。これは感覚的には「物体が重いから」動かないのですが,より正確に言えば,
物体が重い
↓
垂直抗力が大きい
↓
垂直抗力に比例する最大静止摩擦力が大きい
という理屈になります。したがってどんなに重い物体でも,摩擦係数の小さな床面などに置かれていれば非常に小さな力でも引っ張って動かすことができます。
斜面上に置かれた物体はいつ滑るか
よく期末試験や入試問題でこんな設定が見受けられます。角度\(\theta\)の粗い斜面上に物体を置いたところ,物体は斜面上を滑らずに止まっていた,というものです。図にすると次のようになります。
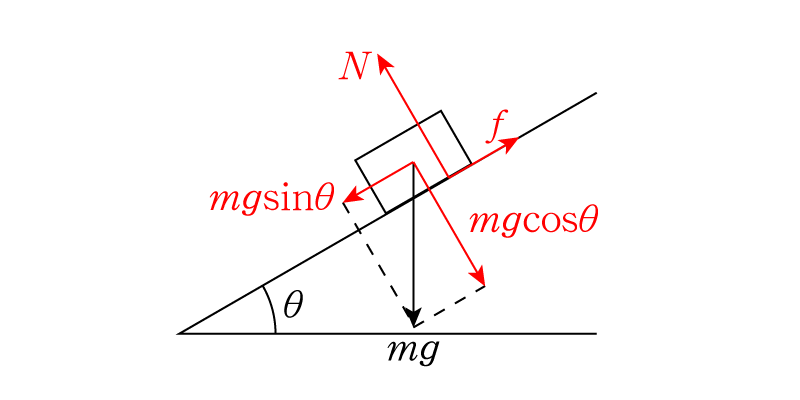
このような状況では物体は次の3つの力を受けています。
- 重力\(mg\)
- 垂直抗力\(N\)
- 静止摩擦力\(f\)
今物体は止まっていますから,力のつり合いが成立しています。力のつり合いは斜辺に平行・垂直な方向それぞれで成立していますから,つり合いの式は次のようになります。\begin{align} N &= mg\cos\theta \\ f &= mg\sin\theta \end{align}この状況下で角度\(\theta\)を増やしていき,斜面を急にしていくと,どこかで耐えられなくなって物体は斜面上を滑り落ちてしまうはずです。物体が滑らない条件は,摩擦力が最大静止摩擦力以下であることですから,最大静止摩擦係数を\(\mu\)と書くと\[ f \leq \mu N\]です。これにつり合いの式を代入すると\[ mg\sin\theta \leq \mu mg\cos\theta\]ですから,整理して\[ \tan\theta \leq \mu\]となります。つまり,物体が滑らない状態を保ちながら急にできる角度は\(\tan\theta = \mu\)を満たす角度までである,ということです。この帰結は非常に有名ですので,頭に入れておくと便利だと思います。

コメント