軸対称や球対称の関数を積分する際に用いられる極座標による積分。図形的イメージからヤコビアンがつくことを理解し,便利に使いこなせるようになりましょう。ここでは被積分関数は全て適当に可積分な実関数とします。
二変数における変換
二変数関数の\(xy\)座標系での積分は次のように計算できます。\[ I = \iint_D f(x,y)dxdy\]この積分を図形的に解釈すると,\(z=f(x,y)\)という曲面と\(xy\)平面で挟まれた領域のうち,\(D\)を底面にもつ部分の体積を求めていることになります。
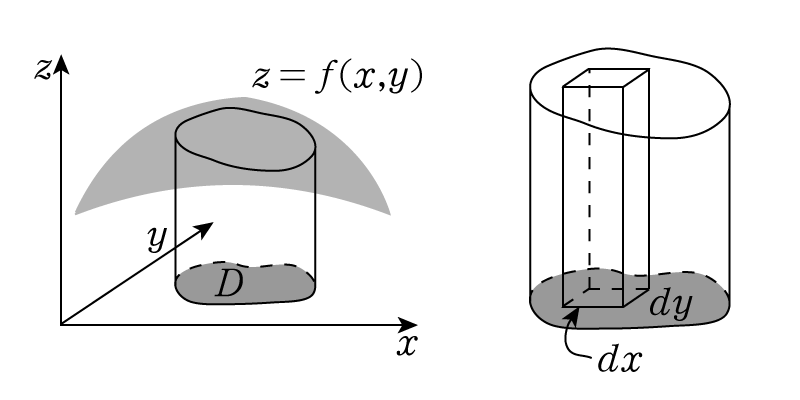
積分の基本的な考え方ですが,その体積は右図のように,\(D\)の中の微小面積\(dxdy\)を底面にもつ微小直方体の体積を集めたもの,と考えます。
ここで,関数\(f\)を次のような極座標変換で変形することを考えます。\[ r = \sqrt{x^2+y^2}, \quad \theta = \tan^{-1}\left(\dfrac{y}{x}\right) \]\(r\)は原点からの距離,\(\theta\)は\(x\)軸正方向から反時計回りに測った角度です。積分の基本的な考え方は変わらないため,微小底面積を持つ直方体の体積を求めることを考えます。ただしこの変形により,微小底面積は\(dx\times dy\)ではなくなり,次の図のように変形されます。
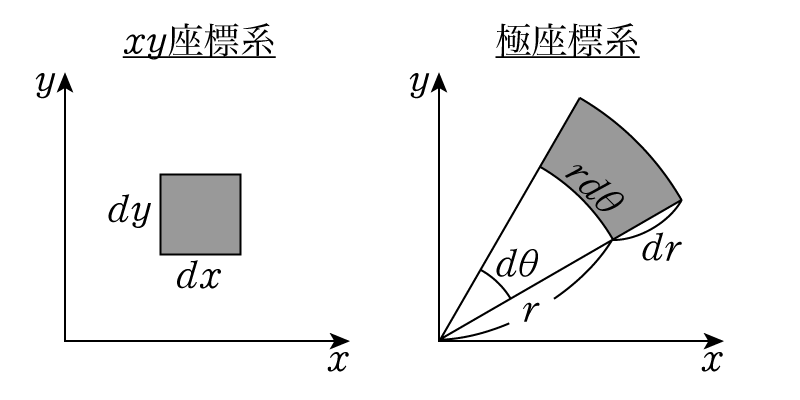
灰色の部分が微小面積ですが,極座標系での微小面積は\(r,\theta\)がそれぞれ微小に変化した際に出てくるものなので図のようになります。図では\(dr\)や\(d\theta\)を大きく描いていますが,実際には非常に小さいので,極座標系においても微小面積は長方形と見なすことができます。つまり,\[ dxdy \to rdrd\theta \]という微小面積の変形が成立します。積分においては\[ \iint_D f(x,y)dxdy = \iint_D f(r,\theta) rdrd\theta \]となります。一見\(dxdy\)が\(drd\theta\)になるような気もしますが,\(r\)という因子がついてきてしまいます。これは変数変換におけるヤコビアンと呼ばれるもので,適切に変換するために必要です。
三変数における変換
三変数関数\(f(x,y,z)\)の領域\(V\)の中での積分を極座標で行うことを考えます。普通に積分すると,\[ I = \iiint_V f(x,y,z)dxdydz\]という三重積分で,微小体積要素は\(dxdydz\)という直方体になります。二変数の時と同様にこれを極座標にしたときの微小直方体の体積を求めることにしましょう。そもそも三次元の極座標とは以下のように定まります。
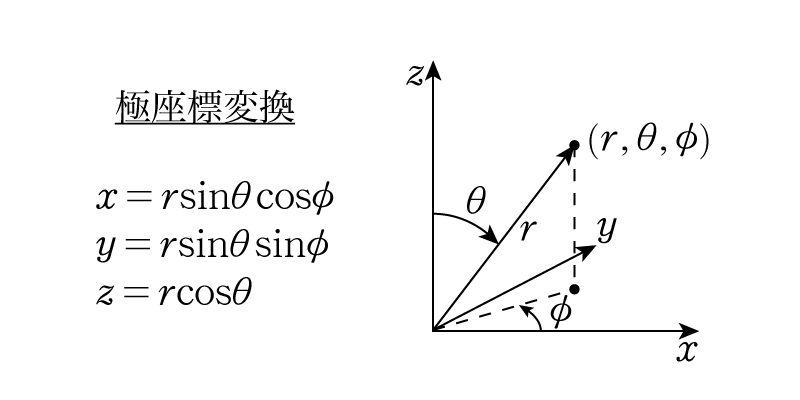
\(r\)は原点からの距離,\(\theta\)は\(z\)軸正方向から測った角度,\(\phi\)は\(x\)軸正方向から測った角度です。この変数変換により,微小直方体は次の図のように変形されます。
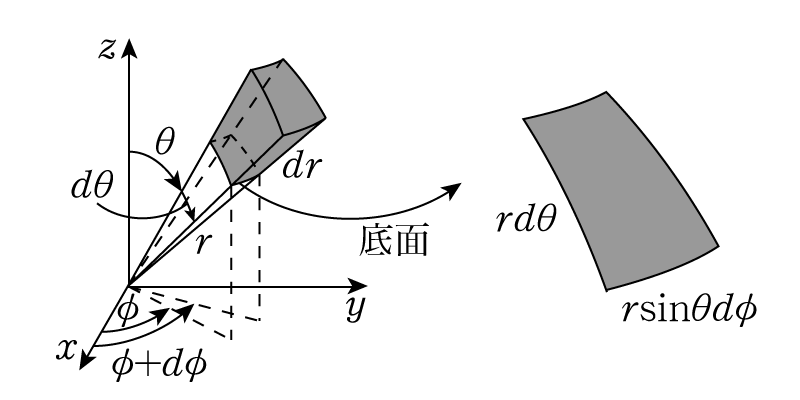
半径方向の\(dr\)を高さとしてみると,底面は右図のように取り出せます。注意したいのは,その底面のうち\(xy\)平面と平行な辺の長さは\(r\sin\theta d\phi\)となることです。これは,極座標変換によって\[ \sqrt{x^2+y^2} = r\sin\theta\]と変形されるためで,二次元の場合とは大きく異なります。したがって微小体積は\[ dxdydz \to r^2\sin\theta drd\theta d\phi\]となり,積分は
と変数変換されます。したがって三次元極座標変換によるヤコビアンは\(r^2\sin\theta\)ということができます。
これを使うと,球の体積は非常に簡単に求めることができます。体積ですから,被積分関数を\[f(r,\theta,\phi)=1\]として積分すれば良いことになります。また,球の半径を\(R\)とすれば,それぞれの変数の積分区間は次のようになります。\[ 0\leqq r \leqq R, \quad 0 \leqq \theta \leqq \pi, \quad 0 \leqq \phi \leqq 2\pi\]これを適用して積分すると,\begin{align} V &= \int_0^R r^2dr \int_0^{\pi} \sin\theta d\theta \int_0^{2\pi} d\phi \\ &= \dfrac{R^3}{3} \cdot 2 \cdot 2\pi = \dfrac{4}{3}\pi R^3 \end{align}という風に球の体積が簡単に求まります。重積分は基本的に,それぞれの変数ごとに積分してやって,最後に掛け算してやれば良いので,基本的な計算は普通の積分と変わりませんね。
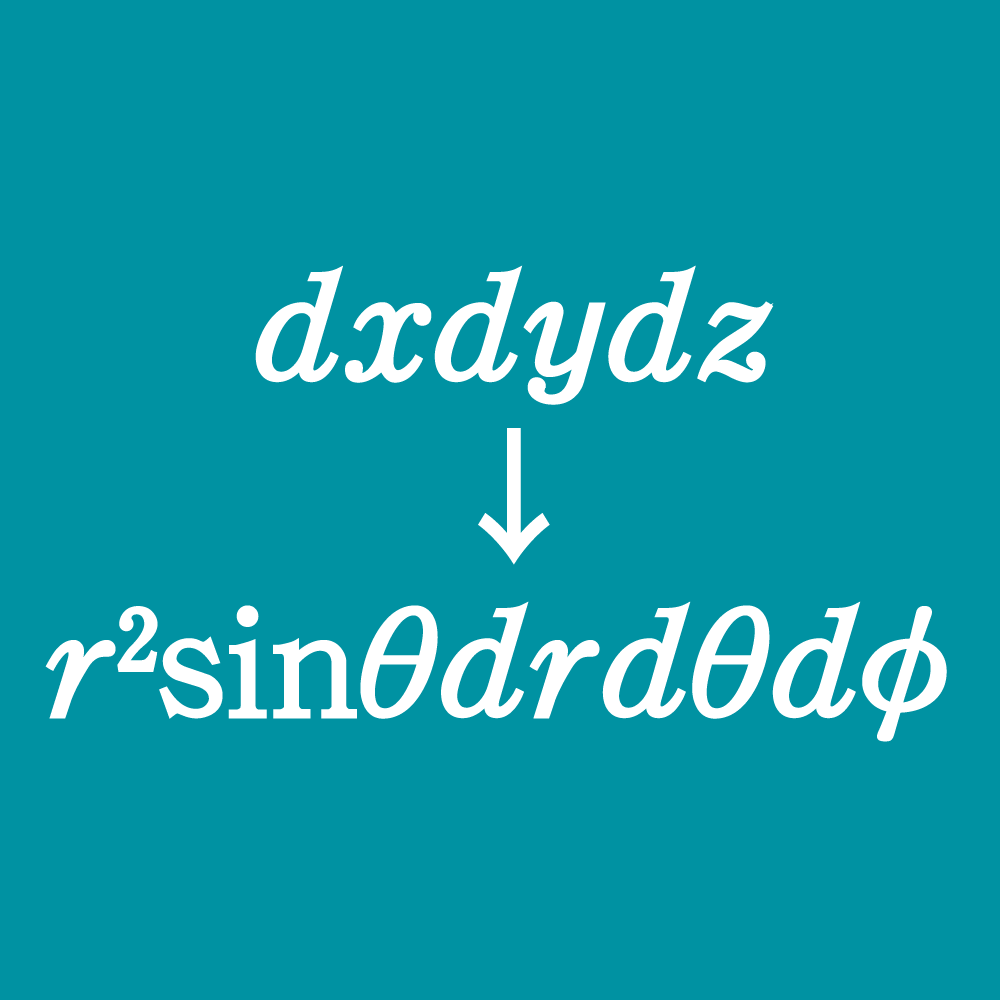
コメント