角運動量と質点の慣性モーメント

運動量と同様に重要な物理量である角運動量。一言で言えば回転の勢いを表す量ですが，その定義とそこから生まれる慣性モーメントという物理量をざっと解説します。

並進運動と回転運動

まず角運動量を考える前に，物体の運動を2種類に分類してみます。

  • 並進運動…物体全体が同じ方向に動く
  • 回転運動…どこかを中心として回る

一つ目の並進運動ですが，これは高校物理でも扱ってきた運動方程式\[m\dfrac{d^2 \vec{r}}{dt^2} = \vec{F}\]によって記述することができます。物体が大きさを持っていても，どの部分も同じ方向に移動しているわけだから，重心の動きだけを考えれば十分という考え方です。

一方の回転運動ですが，これは適当な点（物体の内外部を問わない）を中心に物体が回転する運動です。高校物理では「力のモーメント」という範囲でこの領域の一部分を扱いました。高校レベルでは，大きさをもつ物体が回転しない条件等を考えるだけで実際に物体が回転し出した後を扱いませんでしたが，大学物理ではこれを扱っていくことになります。

それぞれの運動のイメージを図にするとこんな感じです。後のために，上で出てきた並進運動の運動方程式を次のように変形しておきます。\[m\dfrac{d^2 \vec{r}}{dt^2} = \dfrac{d (m\vec{v})}{dt} = \dfrac{d\vec{p}}{dt} = \vec{F}\]式としては全く等価ですが，力が加速度を生み出すという考えから，力が運動量\(\vec{p}\)の時間変化率であるという風に解釈を変更します。

角運動量の定義とその変化

角運動量は回転の勢いを表す量ですが，回転運動はどこを中心に回転してるかの基準（回転軸）が必要です。その中心から物体までの位置ベクトルを\(\vec{r}\)，運動量ベクトルを\(\vec{p}\)とするとき，角運動量\(\vec{L}\)は次で定義されます。

定義：角運動量

\[ \vec{L} = \vec{r} \times \vec{p}\]

つまり定義では，角運動量は位置と運動量の外積で与えられます。例えば，位置も運動量も\(xy\)平面内だった場合は下の図のように\(z\)成分のみをもつ角運動量ベクトルが定義されます。
また外積ですから，その大きさは\(\vec{r}\)と\(\vec{p}\)のなす角を\(\theta\)として\[ |\vec{L}| = |\vec{r}||\vec{p}|\sin\theta\]で与えられますが，図で言うと灰色部分（\(\vec{r}\)と\(\vec{p}\)で張られる三角）の面積の2倍です。さらに運動量は質量と速度の積ということを使えば\[\vec{L} = m\vec{r} \times \vec{v}\]と書き下すこともできます。ここで並進運動の運動方程式\[\dfrac{d\vec{p}}{dt} = \vec{F}\]を思い出しましょう。この式の両辺に左から\(\vec{r}\)を外積として書けると，\[\dfrac{d(\vec{r}\times\vec{p})}{dt} = \vec{r}\times\vec{F}\]となり，この式の右辺を\(\vec{N}\)と書けば\[\dfrac{d\vec{L}}{dt} = \vec{N}\]という角運動量の時間変化を記述する式に変形されます。この式の\(\vec{N}\)はトルク（力のモーメント）と呼ばれ，角運動量を変化させる要因となります。逆の言い方をすれば，トルクが無ければ角運動量は変化せず一定値を取ります。
トルクがないとき，角運動量保存則が成立する。
ではトルクがないとはどういうときでしょうか。もちろん力\(\vec{F}\)が無ければトルクもないのですが，位置ベクトル\(\vec{r}\)と力\(\vec{F}\)が平行であるとき，その外積であるトルクはゼロになります。つまり例えば，回転している物体に対して，回転中心の方向に向かって，もしくは回転中心から離れるように力を加えたとしてもトルクはゼロなので角運動量は変化しないことになります。

角速度ベクトルによる表現

ここで角速度ベクトルという物理量を定義します。そもそも角速度とは速度の角度版，つまり単位時間あたりの角度の変化量を表すのでした。それと全く同じ大きさを持ち，向きを加えたものを新たに角速度ベクトルとして定義します。

定義：角速度ベクトル

角速度ベクトル\(\vec{\omega}\)を位置ベクトル\(\vec{r}\)，速度ベクトル\(\vec{v}\)を用いて次で定義する。\[ \vec{\omega} = \dfrac{\vec{r}\times\vec{v}}{|\vec{r}|^2}\]

すごく難しそうな定義に見えますがやっていることはシンプルです。高校物理でやったようにスカラーの世界では\(\omega = v/r\)で定まるものが角速度でした。このベクトルの定義でも，\(\vec{\omega}\)の大きさはその物体の角速度\(\omega\)に等しいです。それに追加して，向きが外積によって「\(\vec{r}\)から\(\vec{v}\)の向きに右ねじを回して進む方向」と定まります。位置方向の単位ベクトルを\(\hat{r}\)，速度方向の単位ベクトルを\(\hat{v}\)と書くなら，\[\vec{\omega} = \omega(\hat{r}\times\hat{v})\]と書くこともできます。
これを用いて，角運動量ベクトルを表記してみましょう。角運動量ベクトルの定義から次のように変形できます。\[\vec{L} = \vec{r}\times\vec{p} = m\vec{r}\times\vec{v} = mr^2\vec{\omega}\]なお，ここでは原点からの距離\(|\vec{r}|\)を\(r\)と書きました。この変形によって，角運動量は角速度を\(mr^2\)倍したものだとわかりました。この比例定数を（質点の）慣性モーメントと呼び，非常に重要なので\(I\)と表記して回転運動において頻繁に用いる定数となります。

質点の慣性モーメント

以上の議論から次のことが言えます。

質量\(m\)，原点からの距離\(r\)の質点の慣性モーメントは\(mr^2\)で与えられる
この値の意味するところですが，角運動量とトルクの関係を表す式に代入してみるとよくわかります。つまり\[\dfrac{d\vec{L}}{dt} = mr^2\dfrac{d\vec{\omega}}{dt} = I\dfrac{d\vec{\omega}}{dt} = \vec{N} \]となるのですが，これの意味するところは「トルク\(\vec{N}\)を与えたときの角速度変化はトルクを慣性モーメントで割ったものになる」ということです。つまり慣性モーメントは角速度変化のしづらさ，つまり回転のしにくさを表す量だということです。
同じ質量の物体であっても，回転中心から遠ければ遠いほど，それを回すのに必要なトルクが大きいということを意味します。このこと自体は小学校の頃からてこの原理として慣れ親しんできたと思いますが，定量的に扱うとこのような結論となります。ところで，質点を回転させるといってもその方向が一つに定まらないのは気づいたでしょうか。角運動量の説明のときに用いた図では\(z\)軸まわりの回転をしている場合のみ記述しましたが，3次元空間では3つの回転軸を考えることができるはずです。
それぞれの回転軸までの距離は異なるはずですから，一般に質点の座標を\((x,y,z)\)とするなら，
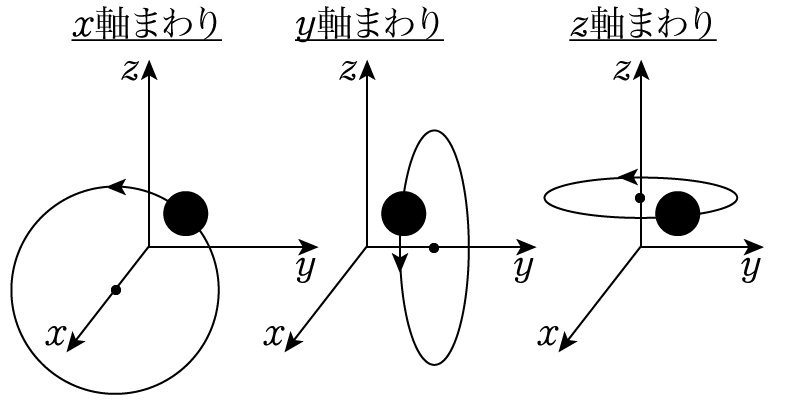
  • \(x\)軸周りの回転 … \(r^2 = y^2+z^2\)
  • \(y\)軸周りの回転 … \(r^2 = z^2+x^2\)
  • \(z\)軸周りの回転 … \(r^2 = x^2+y^2\)

となります。これに応じて，慣性モーメントも回転軸によって値が異なります。それぞれの軸周りの慣性モーメントを\(I_x, I_y, I_z\)と書くことにすると，\begin{align} I_x &= m(y^2+z^2) \\ I_y &= m(z^2+x^2) \\ \quad I_z &= m(x^2+y^2)\end{align}となります。運動量における質量とは異なり，角運動量における慣性モーメントは方向によって異なるテンソルであることは忘れないようにしましょう。

回転の運動エネルギー

最後に回転をしている物体の運動エネルギーについて考えてみましょう。簡単のため速度の大きさ，角速度の大きさをそれぞれ\(v,\omega\)と書くことにすると，運動エネルギーは次のように書けます。\[ \dfrac{1}{2}mv^2 = \dfrac{1}{2} mr^2\omega^2 = \dfrac{1}{2}I\omega^2\]さてここまでくるとだんだんわかってきたと思いますが，並進運動における\(m\)や\(v\)を，回転運動では\(I\)や\(\omega\)に対応させることができます。最後に，並進運動と回転運動で各物理量がどのように対応しているのかを表にまとめましたので，参考にしてみてください。

並進運動 回転運動
運動の勢い \(\vec{p} = m\vec{v}\) \(\vec{L} = m\vec{r}\times\vec{v}\)
運動のしにくさ 質量\(m\) 慣性モーメント\(I\)
エネルギー \(\dfrac{1}{2}mv^2\) \(\dfrac{1}{2}I\omega^2\)
方程式 \(\dfrac{d\vec{p}}{dt} = \vec{F}\) \(\dfrac{d\vec{L}}{dt} = \vec{N}\)

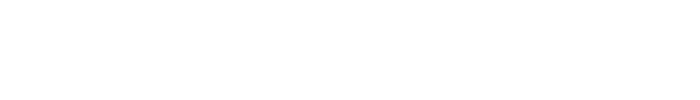
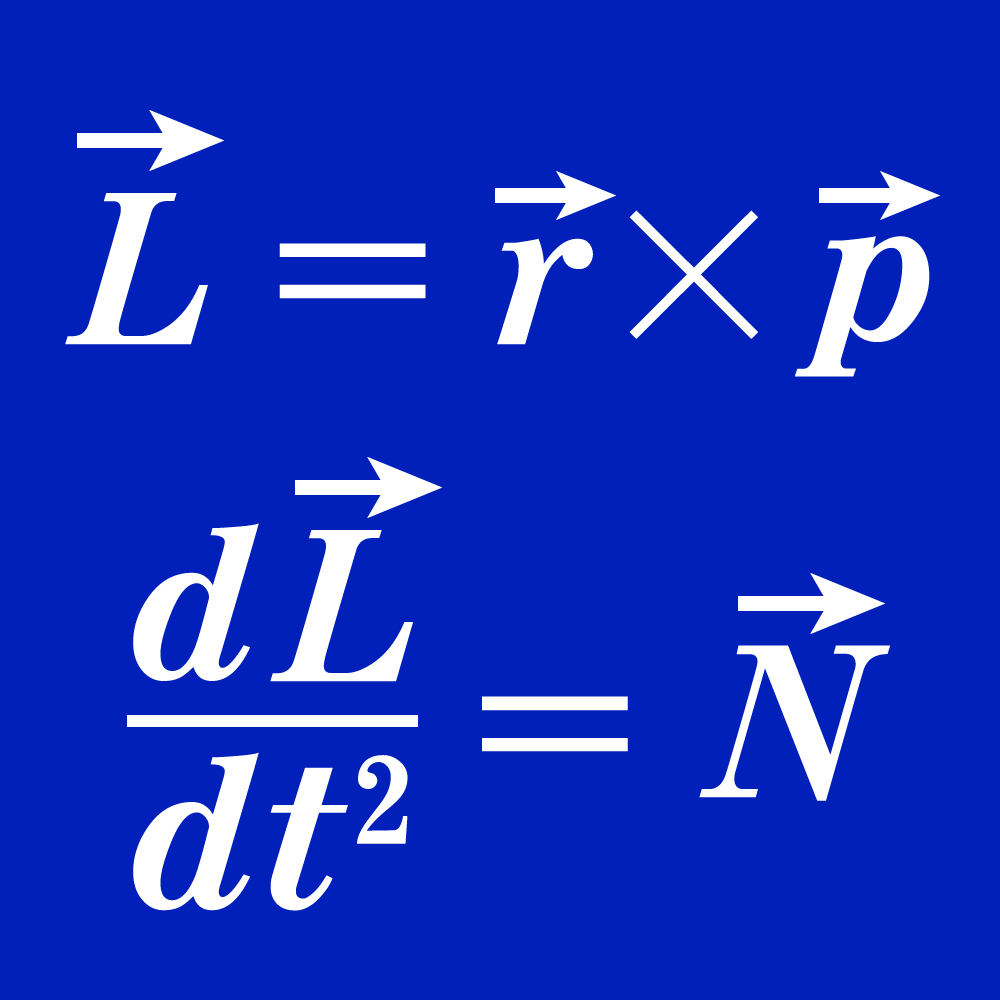
コメント