物理の力学で一番最初に出てくるこの2つの「物理量」。あなたは正確にこれらが何か言えますか?分かっているようで分かりにくい範囲ですが,丁寧に確認していきましょう。
物体の位置はどう定めるのか
普段物体の位置をどのように言及していますか。例えば,
- 机の上のパソコン
- 渋谷のハチ公前で待合わせ
など,相対的に位置を指定していると思います。ただこれは物理で用いるには余りに不正確ですから,ここで数学の助けを借りてきます。中学校で出てきた数直線です。

黒いボールの位置は数直線を置くことによって,万人共通の表現をすることができます。ただし位置を表す数直線を使うときは,
- 原点がどこか定めること(定規の端が動いたら嫌ですよね)
- 正の方向を定めること(定規が急に反対向きになったら測れませんよね)
の2点に気をつけましょう。この図では,「ある時」の位置を原点としましたが,別に「少し後」の位置を原点としても何の問題もありません。その場合は,
\[ ある時:x=-2 \quad 少し後:x=0 \quad そのまた後:x=3\]
と座標がずれることになります。また,この位置の単位ですが,物理では普通メートルを基本として使いますが,原理的には何でも構いません(cmだろうがkmだろうが良いです)。ひとまずメートルということにしておきましょう。
時間の導入
先の例では,「ある時・少し後・そのまた後」と時刻を表現しましたが,これもあいまいですよね?時間も同様に原点(ゼロ時刻)を決めることによって数値で表すことができます。例えば上の例は以下のように書き直すことができます。
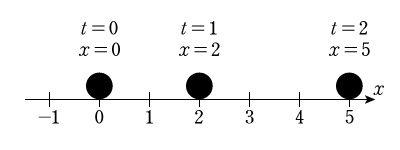
ボールが位置の原点にいるときを時刻の原点とした例です。あくまで一例ですから,時刻はどこを原点にしても構いません。要はどのタイミングでストップウォッチのスタートボタンを押すか,みたいなことです。
時間の単位ですが,普通は秒(second)を基本として使いますが,こちらも原理的には何でも構いません。場合によっては分や時を使うこともあるでしょう。ここでは秒ということにしておきます。
速さの復習
さて,これである時刻における位置を正確に表現できるようになりました。小学校で
\[ 距離 = 速さ \times 時間 \]
という公式を覚えたはずですし,このくらいは日常生活を通じて身についてきたと思います。これを使えば,上の例で\( t=0 \sim 1 \)で速さは一定で,\( t=1 \sim 2\)でも一定だとするとそれぞれ1秒の間に2m,3m動いていますから,それぞれの区間での速さは\(2\mathrm{m/s}\)及び\(3\mathrm{m/s}\)と書けます。つまり,\( t=1 \)で速さが変化したことになります。
ここでもし仮に,このボールを見ている人が\( t=0 \)と\( t=2 \)のところだけしか見ていなかったとしましょう。このとき,この人からすれば2秒間で5m動いたように見えるはずです。すると速さは\( 5 \div 2 = 2.5 \mathrm{m/s} \)となります。
そう,本当は速さは変化していたのに距離を測る時間が長かったために別の速さが出てきました。これを平均の速さと言います。
あまり長い時間間隔で測ると,速さの変化をとらえられずに平均化された速さが出てきてしまうということですね。それに対し,最初求めたように区間ごとの正確な速さを瞬間の速さということがあります。
速度と速さの違い
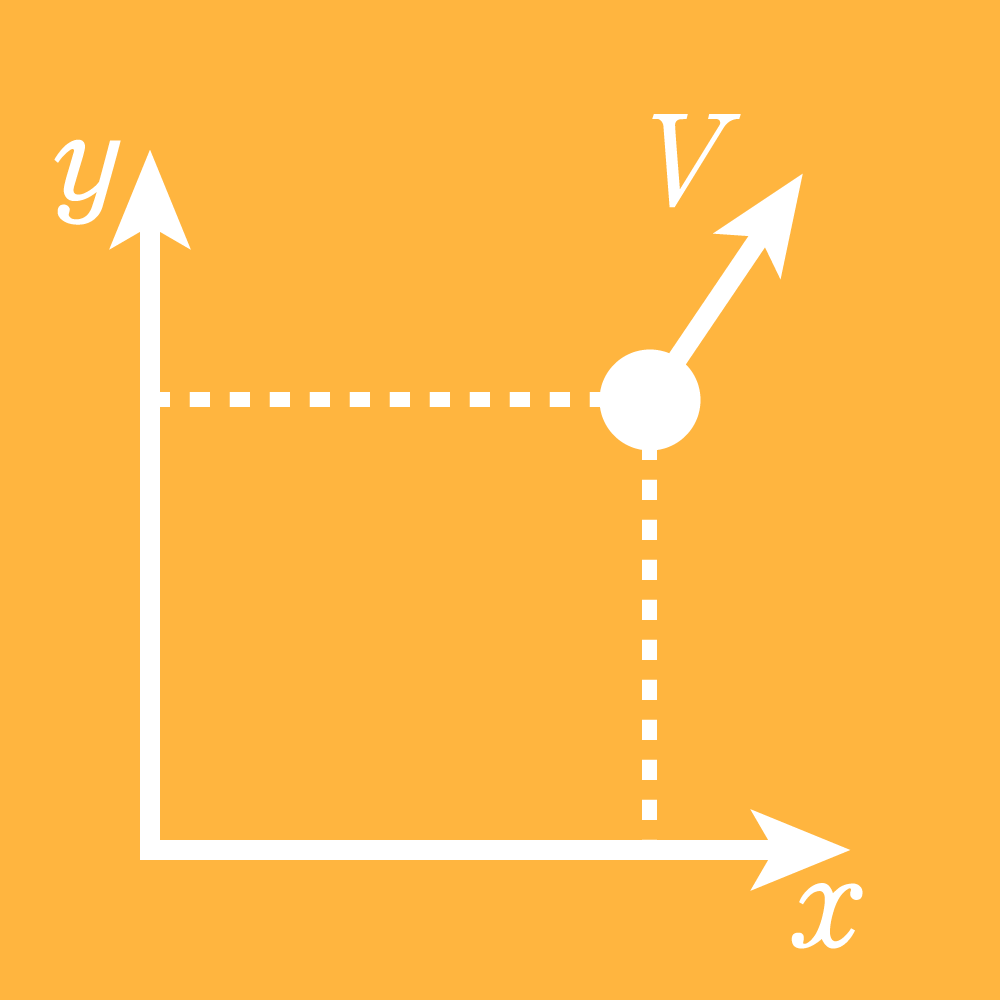
先ほど速さという量を導入しましたが,これは物体がどの方向に動いていても同じように計算できます。一方で速度(こちらの方がより物理では一般的)は次のように定義されます。
より厳密に速度\(v\)を定義すると
グラフを使って考える
一番最初の例に戻って,これまでの内容をまとめてみましょう。位置\(x\)と速度\(v\)は時刻\(t\)によって変わるので,それぞれ横軸を\(t\)としてグラフにすることができます。
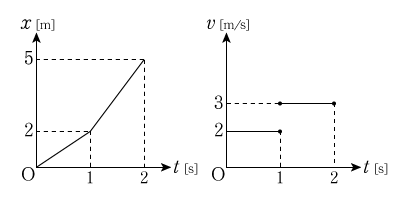
加速度とは何か
読んで字のごとく「加速の度合い」なのですが,数学的には次のように定義できます。加速度は\(a\)と書いて,

まとめ
位置と速度と加速度,この3つは力学で最も基本的な量ですのでしっかり理解できるようにポイントを押さえましょう。ここまでの話をまとめると,
- 位置を指定するときは原点と正の向きを定める
- 速度は位置の時間変化率
- 加速度は速度の時間変化率
- 「速度⇔位置」の関係と「加速度⇔速度」の関係は同じ
というところになりますので,具体的な問題を解きつつ身につけていきましょう。
コメント