ベクトル解析における基本的な操作である勾配,発散,そして回転。ここでは偏微分の知識を前提として,これらの計算方法と解釈を説明していきます。なお,物理の分野では多くの場合我々の住むこの空間について扱いますから,ここではベクトルは3次元のものとします。また以下で用いる関数はすべて適当な回数微分可能であるとします。
微分演算子\(\nabla\)(ナブラ)
まずベクトル解析において初登場するこの演算子。演算子とは何かに作用してそいつを別のものに変えるもののことです。このナブラは\(x,y,z\)軸で決まるデカルト座標系においては,次のように定義されます。
\[ \nabla = \left( \dfrac{\partial}{\partial x}, \dfrac{\partial}{\partial y}, \dfrac{\partial}{\partial z} \right) \]大事なポイントは2つあります。
- 成分を持つベクトルであること
- 各成分が各軸方向の微分作用素であること
微分作用素とは関数に対して作用して,その微分を計算する道具のようなものです。これはベクトルですから,\(x,y,z\)方向それぞれの単位ベクトルを\(\vec{e}_x, \vec{e}_y, \vec{e}_z\)と書けば,\[ \nabla = \vec{e}_x \dfrac{\partial}{\partial x} + \vec{e}_y \dfrac{\partial}{\partial y} + \vec{e}_z \dfrac{\partial}{\partial z} \]と書くこともできます。ナブラはベクトルであることから,その記号の上に矢印を書く人もいますが,ここではめんどくさいので書かないでいきます。どちらにせよ意味は同じです。
勾配(grad)
読んで字のごとく,関数がどれだけの傾き(勾配)を持っているのかをはじき出す計算です。まずは定義から入りましょう。
\[ \nabla f = \mathrm{grad} f = \left( \dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y}, \dfrac{\partial f}{\partial z} \right) \]
1変数関数\(f(x)\)の場合
変数がただ1つのとき,偏微分は普通の常微分と変わらないですから,\[ \nabla f = \vec{e}_x \dfrac{df}{dx} \]となります。これは高校数学でも出てくる普通の微分をベクトル化したものです。
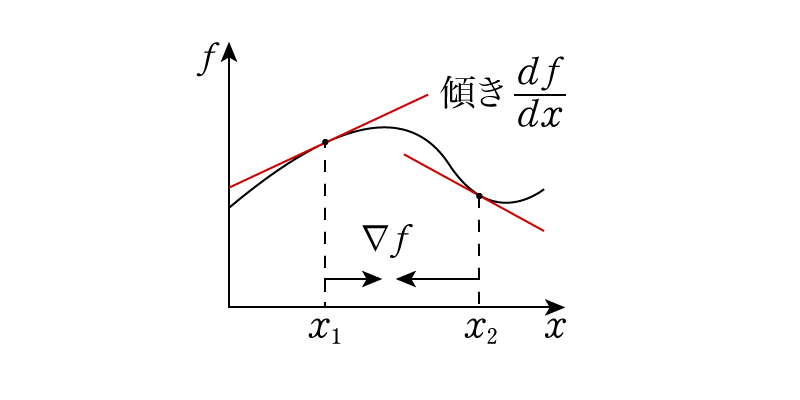
図のように,微分はグラフの傾きを表しますが,勾配はその傾きを大きさに持つベクトルですから,向きを持ちます。マイナスの傾きのところでは,負方向に向くベクトルとなります。すると,勾配ベクトルは必ず関数値が大きいところを向くことになります。例えば,上のグラフの関数が山の断面だったとすると,山の頂上方向を向くベクトルが勾配ということになり,その傾きが急であればあるほどベクトルの大きさは大きくなります。
2変数関数\(f(x,y)\)の場合
次に変数が2つの場合を考えます。このとき,勾配は\[ \nabla f(x,y) = \left( \dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y} \right) \]です。今回は2つの成分をもつベクトルとなります。まずは図を見てみてください。
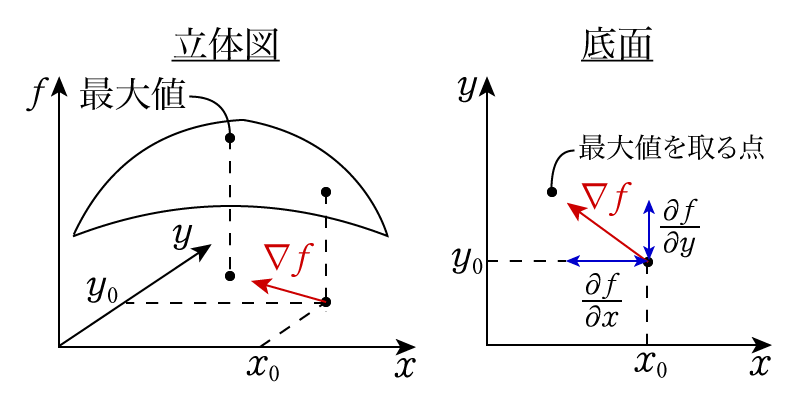
基本的なことは1変数のときと変わりませんが,2変数なので関数を図示すると曲面になります。山の地形などを考えるとこれに相当しますよね。緯度と経度という2つの変数を決めれば標高が決まることから,地形はよく2変数関数の例として用いられます。
この図のように,最大値をとる場所(山で例えれば山頂)があったときに,ある場所\((x_0,y_0)\)における勾配ベクトルは図のように定まります。言葉で書くなら,
- 向きは最大傾斜方向
- 各成分の大きさは各方向の「傾き」
となります。最大傾斜方向とは,その場所から少し動こうとしたときにもっとも曲面の傾きが急な方向という意味です。つまり,この勾配は高校数学で習った微分=傾きという考え方を2次元以上の場合に拡張しているわけです。こう考えると,式だけ見るとややこしそうですが,傾きが急な方向を調べているんだくらいに思えてきませんか。
また,勾配ベクトルの絶対値は\[ |\nabla f(x,y)| = \sqrt{ \left( \dfrac{\partial f}{\partial x} \right)^2 + \left( \dfrac{\partial f}{\partial y} \right)^2 } \]となって「傾きの大きさ」を表しています。2変数関数ですから,傾きを考える際も2成分考えなければいけないですからね。これを使うと,大雑把な議論ですが\(xy\)平面上を微小な距離\(ds\)だけ移動したときの関数\(f\)の変化量は\[ |\nabla f|ds = \sqrt{ \left( \dfrac{\partial f}{\partial x} \right)^2 + \left( \dfrac{\partial f}{\partial y} \right)^2 }\, ds \]と見積もることができます。
3変数関数\(f(x,y,z)\)の場合
最後に変数が3つの場合ですが,次のようになります。\[ \nabla f(x,y,z) = \left( \dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y}, \dfrac{\partial f}{\partial z} \right) \]これを図にすることは難しいです(4次元空間を描画する必要がある)ので,大雑把なイメージだけつかんでもらえれば大丈夫です。なお,3変数関数の例としては気温等があります。緯度,経度だけでなく高度によっても気温は変化しますから,3変数関数となります。図にすることはできませんが,意味合いとしては同じになります。
- ベクトルの向きは関数値が最も大きく変化する方向
- ベクトルの大きさは変化の割合
気温を含む多くの物理的観測量は,3次元空間中で変化しますから,実用上は3変数関数が一番多い気がします。勾配を取っていたら,その量が最も急激に変化する方向を取っているのだな,と思ってください。
発散(div)
これも字の通り,ベクトル場がどれくらい発散しているのかを表す指標で,定義は次の通りです。
\[ \nabla \cdot \vec{A} = \mathrm{div} \vec{A} = \dfrac{\partial A_x}{\partial x} + \dfrac{\partial A_y}{\partial y} + \dfrac{\partial A_z}{\partial z} \]
発散という名前の由来
さて,ベクトル場に対してこのような操作をして出てくるものがなぜ発散と呼ばれるのかを考えてみます。そこで,空間中の微小な直方体を考えてみましょう。
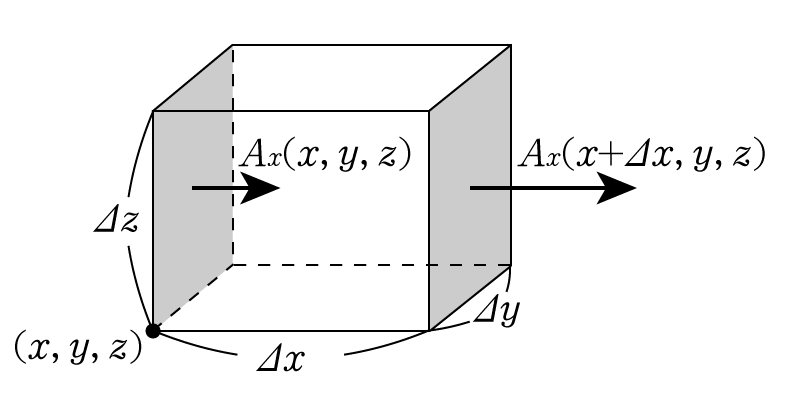
これは\(x,y,z\)軸方向に\(\Delta x, \Delta y, \Delta z\)の辺を持っていて,左手前下の点の座標が\((x,y,z)\)であるような直方体です。一旦簡単のためにベクトル場の\(x\)成分のみ考えることにします。では\(\vec{A}\)を単位面積あたりを通過する水の流量だという風に考えてみましょう。すると,灰色の面を通過する流量はその場所での\(A_x\)に面積\(\Delta y\Delta z\)を乗じればよいから,
- \(x\)の位置を通過する流量は\(A_x(x,y,z)\Delta y\Delta z\)
- \(x+\Delta x\)の位置を通過する流量は\(A_x(x+\Delta x,y,z)\Delta y\Delta z\)
となります。また,水は左から入って右から出ていきますから,この直方体から水が出ていく量は\[\{ A_x(x+\Delta x,y,z) – A_x(x,y,z)\}\Delta y\Delta z\]と書けます。したがって,この出ていく量を直方体の体積で割れば,単位体積当たり出ていく量がわかります。それは,
と書けますが,\(\Delta x \to 0\)の極限を取ることにより,\[ \lim_{\Delta x \to 0} \dfrac{A_x(x+\Delta x,y,z) – A_x(x,y,z)}{\Delta x} = \dfrac{\partial A_x}{\partial x} \]と\(x\)による偏微分となります。全く同じことを\(y,z\)方向にもすることで,それぞれの方向で出ていく水の量は\[ y方向:\dfrac{\partial A_y}{\partial y},z方向:\dfrac{\partial A_z}{\partial z} \]となりますから,結局単位体積の直方体から出ていく水の総量は\[ \dfrac{\partial A_x}{\partial x} + \dfrac{\partial A_y}{\partial y} + \dfrac{\partial A_z}{\partial z} = \nabla \cdot \vec{A}\]と書けます。そしてこれが発散になるのですが,ベクトル場を何かの流れだと意識することで,発散はあるエリアから外に向かって出ていく量を表していることがわかりました。つまりまとめるとこのようになります。
- \(\nabla \cdot \vec{A} > 0\)なら\(\vec{A}\)が湧き出る所がある
- \(\nabla \cdot \vec{A} < 0\)なら\(\vec{A}\)を吸い込む所がある
- \(\nabla \cdot \vec{A} = 0\)なら\(\vec{A}\)の出入りは一定⇒保存される
発散の計算自体は単に偏微分したものの和にすぎませんが,その意味を押さえておくことで電磁気学における電場と磁場の差など,具体的物理現象に応用することができます。
回転(rot)
ベクトル解析最後のツールは回転です。これがたぶん一番直感的理解に苦しむところだと思いますが,まずは定義から。
\[ \nabla \times \vec{A} = \mathrm{rot} \vec{A} = \begin{pmatrix} \dfrac{\partial A_z}{\partial y} – \dfrac{\partial A_y}{\partial z} \\ \dfrac{\partial A_x}{\partial z} – \dfrac{\partial A_z}{\partial x} \\ \dfrac{\partial A_y}{\partial x} – \dfrac{\partial A_x}{\partial y} \end{pmatrix} \]
回転を持たないベクトル場
まずは回転がないベクトル場の例を見ていきます。
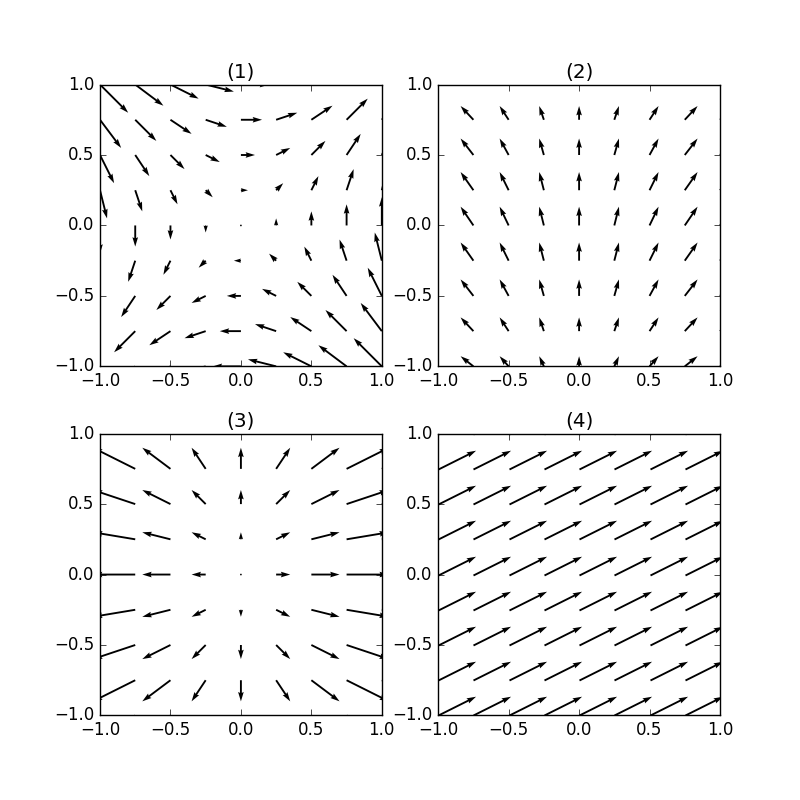
この(1)~(4)のベクトル場はどれも回転を持ちません。特に(1)と(2)なんかは向きが曲がっていますから回転しているように見えますが,計算上ベクトル場の回転はゼロになります。それぞれのベクトル場を与える関数は以下の通りです。\(z\)成分はゼロなので描いていません。
(1) \( \vec{A} = (y,x) \)
(2) \( \vec{A} = (\sin x, \cos y) \)
(3) \( \vec{A} = (2x, y) \)
(4) \( \vec{A} = (2,1) \)
(1)は回転を計算してみると次のようになります。\[ \left[\nabla \times \vec{A} \right]_z = \dfrac{\partial x}{\partial x} – \dfrac{\partial y}{\partial y} = 1-1 = 0\]また(2)と(3)については,\(x\)成分が\(x\)だけの関数,\(y\)成分が\(y\)だけの関数ですから,偏微分がゼロになってしまいます。回転で出てくる偏微分は\(x\)成分の\(y\)微分など,異なる文字同士の微分であることに注意してください。また(4)については定数ベクトル関数ですから,至る所同じ値となり微分がゼロになるため,回転はありません。
回転を持つベクトル場
次に回転をもつベクトル場の例を見ていきます。
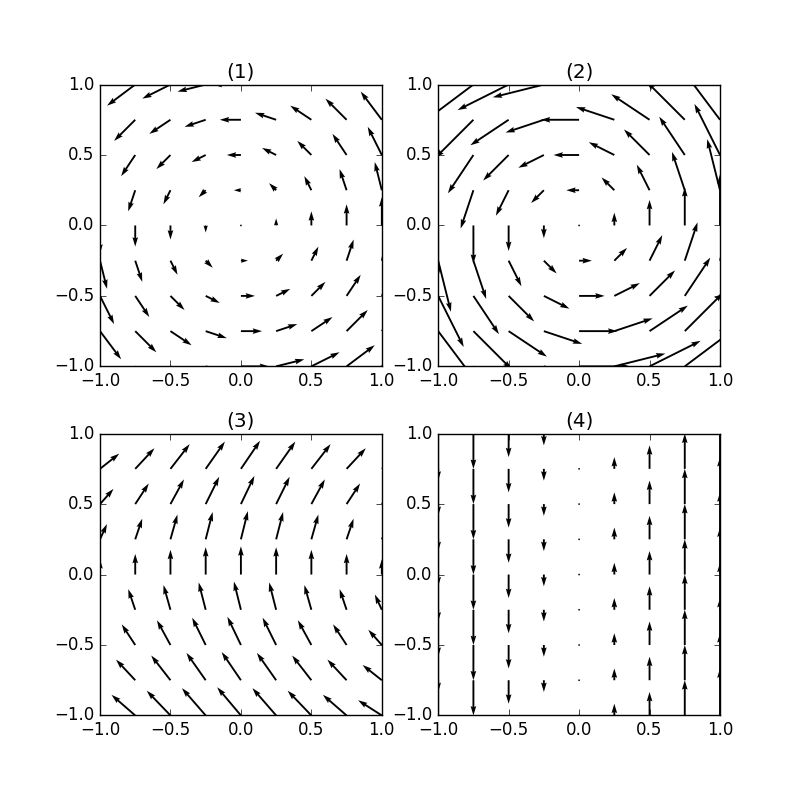
(1)~(3)は見た目がぐるぐる回って見えますね。このようなベクトル場は回転を持ちます。(4)は一見回転が無いようにも思えますが,右半分が上方向に,左半分が下方向に行くことで反時計回りの回転が生まれています。それぞれのベクトル場は次の式で与えられます。
(1) \( \vec{A} = (-y,x) \)
(2) \( \vec{A} = (-y e^{r}, xe^{r}) \quad (r=\sqrt{x^2+y^2})\)
(3) \( \vec{A} = (\sin y, \cos x) \)
(4) \( \vec{A} = (0, 2x) \)
ここで,(1)と(4)の回転ですが,計算してみるとともに2になります。このことベクトル場自体は異なってもその「回転の度合い」は同じと言えます。また,
- 回転が正…反時計回り
- 回転が負…時計回り
にベクトル場が回転します。高校数学のときから反時計回りを正とすることが常だと思いますが,回転でも同様の定義の仕方となります。とにかく回転は図のイメージでとらえるように意識したほうがすんなり理解できると思います。正直\(\nabla\)との外積と言われても私でもピンときません。
まとめ
以上がベクトル解析の基本的ツールである勾配,発散,回転の定義です。少し似ているところもあるので,混同しないように最後に下の表にまとめましたので,参考にしてみてください。
| 勾配 | 発散 | 回転 | |
|---|---|---|---|
| \(\nabla\)の作用するもの | スカラー関数\(f\) | ベクトル場\(\vec{A}\) | ベクトル場\(\vec{A}\) |
| 表記 | \(\nabla f\) | \(\nabla \cdot \vec{A}\) | \(\nabla \times \vec{A}\) |
| 別表記 | \(\mathrm{grad}f\) | \(\mathrm{div}\vec{A}\) | \(\mathrm{rot}\vec{A}\) |
| 計算結果 | ベクトル場 | スカラー関数 | ベクトル場 |
| 結果の解釈 | 最大傾斜方向 | 湧き出しor吸い込み | 流れの回転 |

コメント
回転を持つベクトル場の例の
(4) A =(2x,0)
は
(4) A =(0, 2x)
ではないでしょうか?
たなかさん
コメントありがとうございます。
ご指摘の通り、誤りでしたので修正いたしました。
修正ありがとうございました。
回転をもつ、もたないの4つずつの例示のおかげでものすごく理解しやすかったです。
自分でも例示の式から図を起こしていて気づきました。