高校物理の電磁気学で最初に学ぶこの概念。きちんと理解していないといつまで経ってもあやふやなままですから,定義を自分で言えるように確認しましょう。
クーロンの静電気力を理解しよう
電場について学ぶ前に,まず電磁気力の基本的なものであるクーロン力について学びましょう。距離\(r\)離れた2つの物体がそれぞれ\(Q,q \,[\mathrm{C}]\)の電荷(電気量)を持っているとき,その2者には力\(F\)が働きます。その大きさは次のように表せます。
ここで\(k\)はクーロンの比例定数です。勘の良い人は気づくと思いますが,これは万有引力の式の形とそっくりですよね。万有引力の質量を電荷に,万有引力定数をクーロンの比例定数に変えただけです。ただし一つだけ万有引力とは異なり注意すべき点があります。それは
- \(Q\)と\(q\)が同符号なら斥力(お互いを反発しあう力)
- \(Q\)と\(q\)が異符号なら引力(お互いを引きあう力)
ということです。中学校でもプラスの電気とマイナスの電気が引き合う,という初歩的なことはやると思いますが,高校以上ではそれをより定量的に式で評価する必要があります。万有引力の式に出てくる質量はマイナスになりえませんが,電荷はマイナスもありうることからこの違いが出てきます。
電場という考え方
さて,クーロン力がわかったところで電荷\(q\)の物体の気持ちになってみましょう。自分自身の電荷が大きくなればなるだけ,受けるクーロン力も大きくなりますよね。ただその力を生み出しているのは相手の電荷\(Q\)です。相手の影響だけを残して,自分の電荷の大小に左右されない量を作り出しておいた方が便利ですから,さっきの力を自分の電荷\(q\)で割ってみましょう。実はこれがクーロン電場の定義で,
\[ E = k\dfrac{Q}{r^2} \]
です。電場はよく\(E\)という文字で表されます。これは電荷\(Q\)が作り出した「場」で,その影響を受ける対象が何であれ絶対的に存在するものです。
このように背景のように存在して,何か物体が来るとそれに力を及ぼすようなものを場といいます。例としては重力がそうで,例えば地球上なら質量\(m\)の物体は\(mg\)の重力を受けますよね。これは大きさ\(g\)の重力場がある,と解釈することができます。
いま電場を求めるときに,(クーロンの)静電気力を電荷で割りましたから,逆に次のことが言えます。
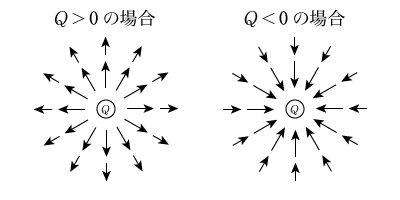
- 正の電荷は放射状に広がる電場
- 負の電荷は自身に収束する電場
という特徴があります。いずれも電場の大きさ自体は距離で減衰しますから,図上でも矢印は短くなっていきます。電場は単位電気量(\(1\mathrm{C}\))が受ける静電気力とも解釈できますから,\(1\mathrm{C}\)の電荷は正の電荷と反発し,負の電荷とは引き合うことから,それぞれの電場が広がるのか・まとまるのかの違いは理解できると思います。このように位置によってベクトルの向きも大きさも異なるような場を特にベクトル場と呼びます。
また電場はベクトル量ということから,ベクトルの足し算をすることができます。つまり,2つの電場\(\vec{E}_1, \vec{E}_2\)が存在した場合,その合計\(\vec{E}\)は次のような足し算になります。
2つほど例を挙げておきましたが,要はベクトルの足し算ですから図的には平行四辺形の斜辺になるし,もし\(x\)軸や\(y\)軸などが設定されていて電場の軸方向の成分が計算できるなら,成分ごとの足し算をすれば良いです。
[応用] 2つの電荷が作る電場を合成する
これまでの考え方を応用して2つの電荷が作る電場の足し算をして,結果としてどのような電場が生じているのかを調べて見ましょう。実際に計算するために\(xy\)平面で考えます。今回は,
- \((-a,0)\)に正の電荷\(Q\)が固定されている
- \((a,0)\)に負の電荷\(-Q\)が固定されている
としましょう。この時位置\((x,y)\)に作られる電場を計算します。とりあえず,どんな感じに電場が作られるのか見てみましょう。
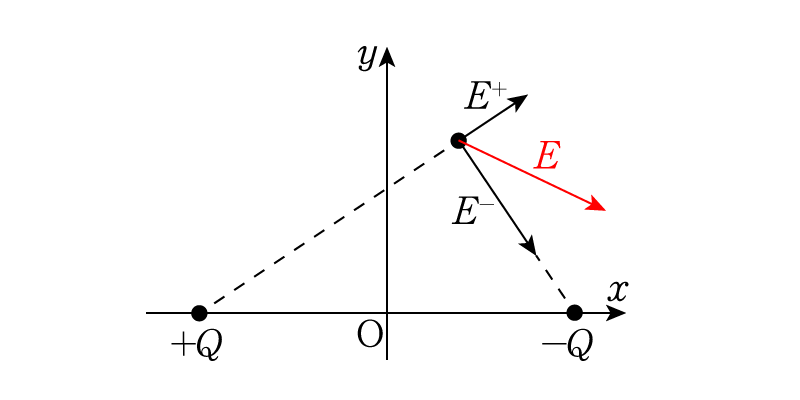
正の電荷が自分から突き放すように,負の電荷が引き込むように電場を作っていますね。また,図に示した点では負の電荷の方が近いですから,負の電荷が作る電場の方が大きいです。では実際に計算していきます。まず正の電荷がここに作る電場\(\vec{E^{+}} = (E^{+}_x, E^{+}_y)\)は次のように書けます。
\begin{align*}
E^{+}_x &= k\dfrac{Q}{(x+a)^2+y^2} \cdot \dfrac{x+a}{\sqrt{(x+a)^2+y^2}} \\
E^{+}_y &= k\dfrac{Q}{(x+a)^2+y^2} \cdot \dfrac{y}{\sqrt{(x+a)^2+y^2}}
\end{align*}
クーロン力の後ろにそれぞれ掛け算されているのはベクトルの大きさを成分に分解するための\(\cos\theta,\,\sin\theta\)に相当します。同様にして負の電荷が作る電場\(\vec{E^{-}} = (E^{-}_x, E^{-}_y)\)は次のように書けます。
\begin{align*}
E^{-}_x &= -k\dfrac{Q}{(x-a)^2+y^2} \cdot \dfrac{x-a}{\sqrt{(x-a)^2+y^2}} \\
E^{-}_y &= -k\dfrac{Q}{(x-a)^2+y^2} \cdot \dfrac{y}{\sqrt{(x-a)^2+y^2}}
\end{align*}
合成された電場はこれらを成分ごとに足し算してあげれば良いから,最終的に作り出される電場\(\vec{E} = (E_x, E_y)\)は次のように書けます。
\begin{align*}
E_x &= kQ \left[ \dfrac{x+a}{\{(x+a)^2+y^2\}^{3/2}} – \dfrac{x-a}{\{(x-a)^2+y^2\}^{3/2}} \right]\\
E_y &= kQ \left[ \dfrac{y}{\{(x+a)^2+y^2\}^{3/2}} – \dfrac{y}{\{(x-a)^2+y^2\}^{3/2}} \right]
\end{align*}
これをイメージ図で書くとこのようになります。
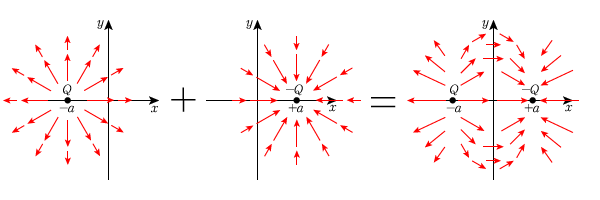
合成後のベクトルは長さ・向きともにだいたいのイメージです。正電荷から出た電場が負の電荷に吸い込まれるように入っていくのが分かります。大体で良いので,このようなイメージを持っておくと良いでしょう。というのも,電場はそこに正の電荷を置いた時の力の向きに一致しますから,頭に入れておくと運動のイメージがつきやすくなります。
一様な電場について
今まで考えてきた電場は位置によって向きも大きさも違うものでしたが,時にどこでも向きも大きさも同じ電場を考えることがあります。このような電場を一様電場と言います。先のクーロン電場でも,非常に狭い範囲だけに着目するなら電場にさして差はありませんから一様電場と見なすこともできます。
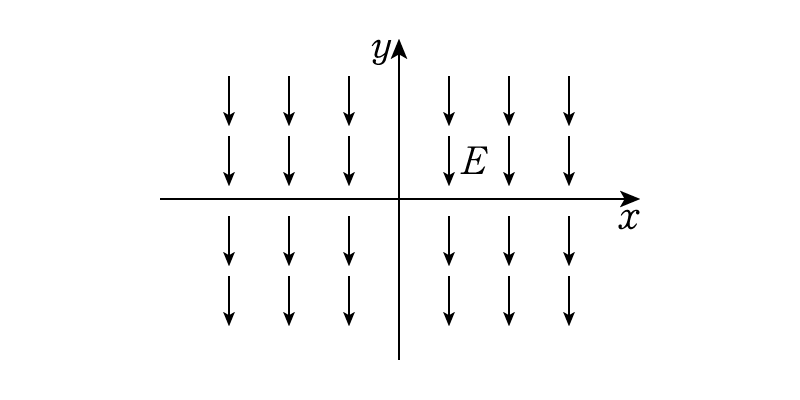
図に示すと上のようになります。どこでも大きさ\(E\)の電場が\(y\)軸下向きに存在している様子です。電場の定義から,この状態では電荷\(q\)をどこに置こうがその電荷は\(qE\)という大きさの力を受けることになります。これこそ重力と同じですね。
もちろん一様な電場についても,ベクトルの足し算によって一様な電場同士,また一様な電場とクーロン電場などの足し算をすることは可能です。
まとめ
いかがだったでしょうか。ここではクーロン力により生じるクーロン電場と一様な電場について解説しました。どちらも電場の定義は同じですから,少し電磁気学に苦手意識があるなあという人は力学における重力または万有引力と結びつけて考えるとスッキリするかもしれません。一番気を付けてほしいのは,負の電荷を電場中に置いた場合は電場と正反対の方向に力を受けるということです。あとは実際に問題を扱いながら慣れていきましょう。


コメント