マクスウェル方程式の意味

2019年02月06日

電磁気学の基本を記述する支配方程式であるマクスウェル方程式。たった4本の式で電磁気現象のほぼすべてを説明できる強力なものですが，式の形とその解釈をじっくり見ていきましょう。大学レベルですが，ニュアンスだけなら高校生でも理解できるように書いたつもりです。

まず方程式を眺めてみよう

何はともあれマクスウェル方程式がどんなものか見てみましょう。様々な書き方がありますが，ここでは電場\(\vec{E}\)と磁束密度\(\vec{B}\)について記述します。以下では\(\varepsilon\)：誘電率と\(\mu\)：透磁率の2つの物理定数を用いています。

  1. \( \nabla \cdot \vec{E} = \dfrac{\rho}{\varepsilon} \)
  2. \( \nabla \cdot \vec{B} = 0 \)
  3. \( \nabla \times \vec{E} = -\dfrac{\partial \vec{B}}{\partial t} \)
  4. \( \nabla \times \vec{B} = \mu\varepsilon \dfrac{\partial \vec{E}}{\partial t} + \mu\vec{j}\)

ここでは，それぞれの式の意味を簡単な文章で書くならこのようになります。

  1. 電場は電荷があるところから湧いて出てくる
  2. 磁場がどこかから湧き出ることはない
  3. 磁場が時間変化すると電場は回転を持つ
  4. 電場の時間変化と変位電流によって磁場は回転を持つ

おいおい「簡単な文章」って言ったくせに，1と2はともかく3と4はなんだ，となりますよね。このベクトル場の回転という考え方はベクトル解析で用いられるものですが，少しとっつきにくいと思います。下のページでベクトル解析について詳説していますので、気になる方はこちらを先にお読みいただければと思います。

ベクトル解析：勾配と発散と回転
ベクトル解析における基本的な操作である勾配，発散，そして回転。 ここでは偏微分の知識を前提として，これらの計算方法と解釈を説明していきます。
physics-school.com
2019年02月07日

なお，この1～4にはそれぞれ名前が付されています。3は微妙ですがそれ以外は人の名前を取って名付けられていて高校レベルで出てくるものもあります。

  1. ガウスの法則
  2. 磁荷非存在の法則
  3. ファラデーの電磁誘導の法則
  4. アンペールの法則

以下ではそれぞれについて見ていくことにしますが，上のような表し方は微分形式と呼ばれローカルで綺麗な式ですが，解釈においては適当な領域で積分してあげた積分形式の方が見やすいこともあります。そのため，以下ではどちらも併用しながら解説していきます。

ガウスの法則

まずこの式は，電場の発散が電荷密度に比例することを主張しています。ここで\(\rho\)は電荷密度で，単位体積当たりの電気量を意味します。また\(\varepsilon\)は誘電率という定数です。\[ \nabla \cdot \vec{E} = \dfrac{\rho}{\varepsilon} \]高校物理で習う通り電場は電荷があればそこから湧き出ていましたよね。正電荷から湧き出て，負電荷に吸い込まれていたと思います。

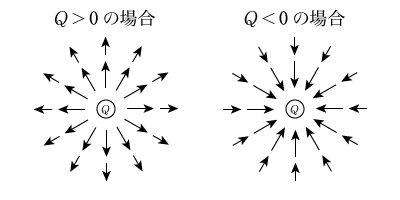
右辺の\( \nabla \cdot \vec{E}\)は発散ですから，正電荷なら発散がプラスで，負電荷ならマイナスですからイメージに合致すると思います。とはいえ少しわかりづらいので適当な領域\(V\)で両辺を積分してみましょう。\[ \int_V  \nabla \cdot \vec{E} \, dv = \dfrac{1}{\varepsilon} \int_V \rho \, dv \]右辺の積分は，単位体積当たりの電気量を体積で積分しているわけだから，ある領域（球体でも直方体でも）の中にある電荷の総量になります。左辺ですが，次のベクトル解析における定理を用います。

～ガウスの定理～
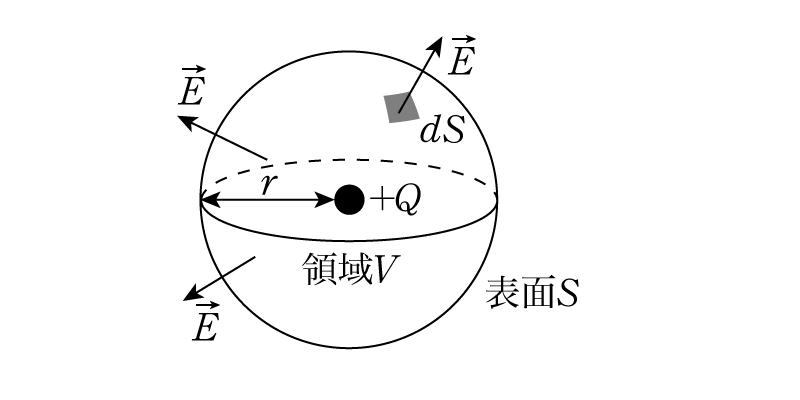
表面\(S\)をもつ閉じた領域\(V\)に対して，任意のベクトル場\(\vec{A}\)は次を満たす。
\[ \int_V \nabla \cdot \vec{A} \, dv = \int_S \vec{A} \cdot \vec{n} \, dS \]
この定理の証明を含む詳細は上記のベクトル解析のページを参考にしてください。これを使うことによって，電場の発散の空間積分が，電場の面積分に変わります。つまり，\[ \int_V \nabla \cdot \vec{E} \, dv = \int_S \vec{E} \cdot \vec{n} \, dS \]ですから，ガウスの法則の積分形式は次のように書けます。\[ \underbrace{\int_S \vec{E} \cdot \vec{n} \, dS}_{電場を領域表面で面積分したもの} = \dfrac{1}{\varepsilon} \underbrace{\int_V \rho \, dv}_{領域内の総電荷} \]電場の面積分というと難しく聞こえますが，要は面を垂直に貫く電場の大きさ×面積です。これを使うことによって，クーロンの静電気力の大きさを説明することができます。
例えば図のように，正電荷\(+Q\)が作り出す電場\(\vec{E}\)を考えたとき，向きは等方的に電荷を中心とする半径方向になりますが，その大きさはガウスの法則から求まります。この場合の電場の面積分は，距離\(r\)においては一定のはずですから，電場の半径成分を\(E(r)\)と書くと，\[ \int_S \vec{E} \cdot \vec{n} \, dS = \underbrace{4\pi r^2 \cdot E(r)}_{球の表面積×電場} \]となります。また，この球の領域内にある電荷は\(+Q\)のみですから，ガウスの法則から，\[ 4\pi r^2 \cdot E(r) = \dfrac{Q}{\varepsilon} \quad つまり \quad E(r) = \dfrac{1}{4\pi\varepsilon}\cdot\dfrac{Q}{r^2} \]と求まります。これは，クーロンの静電気力と公式と一致しますね。

磁荷非存在の法則

この世界に単一の磁荷が存在しない，ということを意味します。例えば，磁石を例にとって考えると，必ずN極とS極がペアになって存在していて，N極だけの磁石やS極だけの磁石は絶対に存在しません。ですから，磁場は必ずN極から出てS極に入り，どこからの点で湧き出たり収束することはありません。

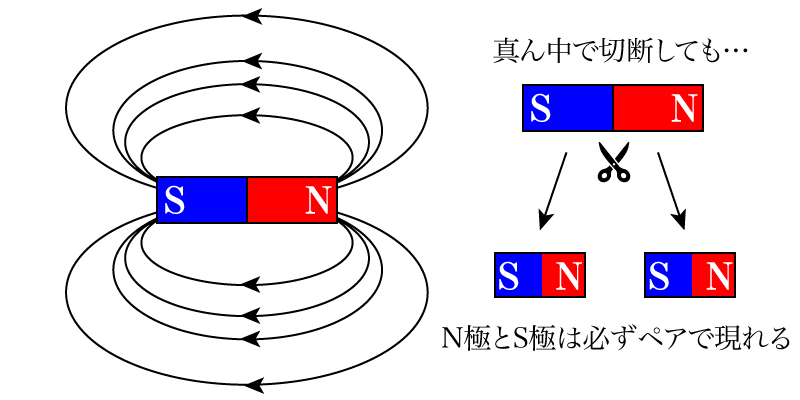
つまり，任意の領域\(V\)についてそこに入ってくる磁力線と，出ていく磁力線は必ず等しいことになります。ガウスの定理を使って積分形式を作るなら，下のようになります。\[ \int_V \nabla \cdot \vec{B} \, dv = 0 \]この式に限っては，意味をきちんと説明できれば十分です。

ファラデーの電磁誘導の法則

この法則自体は高校物理でも出てきましたね。高校物理では，回路などで囲まれた部分を貫く磁束を\(\Phi\)として，誘導起電力\(V\)が，\[ V = -\dfrac{d\Phi}{dt} \]と書けるというものでした。この負号は磁束の変化に逆らって起電力が生じる，というレンツの法則を表していました。上で紹介した微分形式も実は同じことを主張しています。任意の閉曲線\(C\)で囲まれた曲面\(S\)を考えましょう。この面\(S\)上で，微分形式\[ \nabla \times \vec{E} = -\dfrac{\partial \vec{B}}{\partial t} \]を面積分します。つまり，\[ \int_S ( \nabla \times \vec{E} ) \cdot \vec{n} \, dS = – \int_S \dfrac{\partial \vec{B}}{\partial t} \cdot \vec{n} \, dS \]です。右辺の時間微分と積分を入れ替えて，\[ 右辺 = -\dfrac{\partial}{\partial t} \int_S \vec{B} \cdot \vec{n} \, dS \]ですが，これは磁束密度の面積分ですから，閉曲面\(S\)を垂直に貫く磁束密度を集めたものを表します。これが磁束の定義ですから，\[ 右辺 = -\dfrac{\partial}{\partial t} \int_S \vec{B} \cdot \vec{n} \, dS = -\dfrac{\partial \Phi}{\partial t} \]となります。次に左辺ですが，ここでまたベクトル解析の定理を用います。

～ストークスの定理～
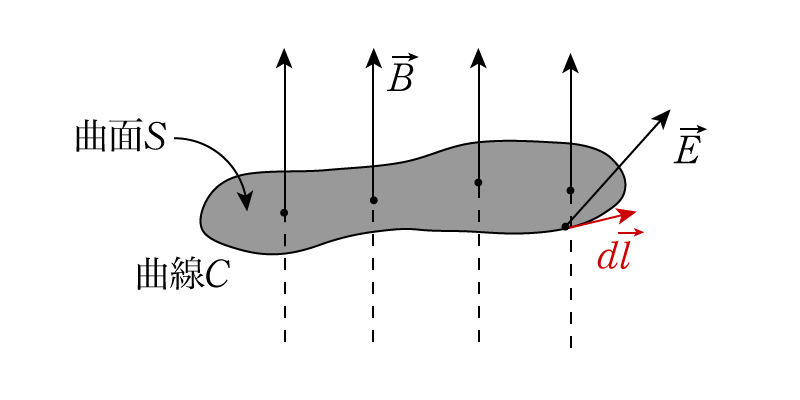
周曲線\(C\)をもつ閉じた曲面\(S\)に対して，任意のベクトル場\(\vec{A}\)は次を満たす。
\[ \int_S (\nabla \times \vec{A}) \cdot \vec{n} \, dS = \int_C \vec{A} \cdot \, d\vec{l} \]
つまり，あるベクトル場の回転の面積分は，その境界の曲線上での線積分に一致するということです。なお，線積分するループの回る方向は，その方向が面積分の\(\vec{n}\)と右ねじの法則をなすように取ります。これを使うことで，左辺の積分は電場の線積分に変わります。したがって，ファラデーの電磁誘導の法則は次のように表されます。\[ \underbrace{\int_C \vec{E} \cdot \, d\vec{l}}_{電場を境界上で線積分したもの} = -\underbrace{\dfrac{\partial \Phi}{\partial t}}_{磁束の時間変化率} \]さらに，電位は電場を曲線上に沿って積分した値であることを考えれば，この左辺はループ全体の起電力を表すことになります。したがって，この微分形式のファラデーの法則も高校物理で学習したものに相違ないことがわかりましたね。
なお，今回の閉曲面\(S\)は別に平面でなくともよいので，原理的にはどんなにぐにゃぐにゃの回路を作っても成立します。ただしその場合は\(\vec{n}\)が様々な方向を向くために，磁束密度の面積分の計算が極めて困難になることに注意してください。
この図のように，ある面に着目してそこを貫く磁束密度を考えます。一般に，\(\vec{B}\)と\(\vec{n}\)や\(\vec{E}\)と\(d\vec{l}\)は直交するとは限らないので，必ず内積ということを意識してください。

アンペールの法則

まずこの式をよく見てみてください。\[ \nabla \times \vec{B} = \mu\varepsilon \dfrac{\partial \vec{E}}{\partial t} + \mu\vec{j}\]左辺と右辺第1項はファラデーの電磁誘導の法則において\(\vec{E}\)と\(\vec{B}\)を入れ替えて符号を変えただけですね。ところが右辺第2項に\(\vec{j}\)というベクトルが付けられています。これは電流密度ベクトルで単位面積あたりを貫く電流を表しています。マクスウェル方程式におけるこの項は特に変位電流と呼ばれていて，非常に大きな意味を持ちます。まずは適当な閉曲面\(S\)で面積分をしてみましょう。先と同じようにストークスの定理を用います。すると，\[ \int_C \vec{B} \cdot \, d\vec{l} = \mu\varepsilon \dfrac{\partial}{\partial t} \int_S \vec{E} \cdot \vec{n} \, dS + \mu J \]です。閉曲面を通過する電流をまとめて\(J\)と書いています。電磁波を知っていれば，電場が時間変化すれば磁場も変化する，ということをわかっているでしょうから，右辺第1項は納得できると思います。後ろの電流の項は，高校物理でも出てきたアンペールの法則を表します。

もし電場に時間変化が無ければ時間微分の項が消えますから，\[ \int_C \vec{B} \cdot \, d\vec{l} = \mu J \]となりますが，さらにここで磁場\(\vec{H}\)を\(\vec{H}=\vec{B}/\mu\)で定義すると，\[ \int_C \vec{H} \cdot \, d\vec{l} = J \]です。つまり磁場をループに沿って積分すると，そのループの内側を通る電流の総量に一致するということです。もっとも簡単な例を考えてみましょう。

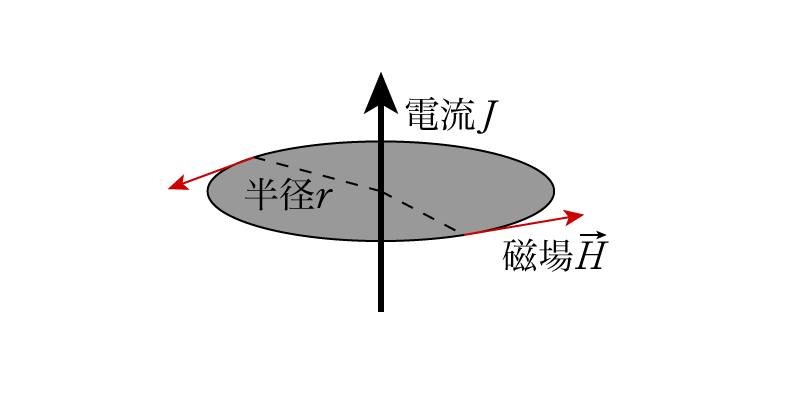
半径\(r\)の円形ループの中心を電流\(J\)が貫いているとき，円周上の磁場は向きが反時計回りで値は一定ですから，線積分の値は\[ \underbrace{2\pi r}_{ループの長さ} \times \underbrace{H(r)}_{距離rでの磁場の強さ} \]と表されます。ゆえにその磁場の大きさは\[ 2\pi r \cdot H(r) = J \quad ゆえに \quad H(r) = \dfrac{J}{2\pi r} \]です。この結論自体は高校でもやりましたね。このように平易な状況なら多くの場合でループ上で磁場の大きさが一定になるため，線積分は単純に磁場×ループの長さとなって簡素化されます。

積分形式のまとめ

それぞれの式を微分した形をまとめます。

  1. \( \displaystyle \int_S \vec{E} \cdot \vec{n} \, dS = \dfrac{1}{\varepsilon} \int_V \rho \, dv \)
  2. \( \displaystyle \int_V \nabla \cdot \vec{B} \, dv = 0 \)
  3. \( \displaystyle \int_C \vec{E} \cdot \, d\vec{l} = -\dfrac{\partial \Phi}{\partial t} \)
  4. \( \displaystyle \int_C \vec{B} \cdot \, d\vec{l} = \mu\varepsilon \dfrac{\partial}{\partial t} \int_S \vec{E} \cdot \vec{n} \, dS + \mu J \)

これから先マクスウェル方程式を変形して波動方程式を作ったり，相対論に取り込むときはやはり微分形式を用いるのですが，それぞれの式を丸暗記するだけでなく，積分形式にして意味や解釈を理解することが非常に重要になってきます。大学レベルの初等電磁気学で多くの人がとりあえず頭に入れ込んで試験に臨んでいますが，将来のためにも何度もこの記事を読んで理解するようにしましょう。

コメント