東京大学2019年度入試の物理第1問の解説ページです。問題のPDFファイルはこちらからダウンロードできます。なお,問題そのものの著作権は東京大学に帰属します。ご注意ください。
設問Ⅰ
加速度運動をする台車およびその台車の上でバネ運動をする物体に関する問題です。台車の位置を測る\(x\)座標と,物体の位置を測る台車に固定された非慣性系の\(y\)座標が共存することに注意が必要です。時間の尺度として,\[ T = 2\pi \sqrt{ \dfrac{m}{k} }\]と言うバネの振動周期が与えられています。
小問(1)
表1−1に与えられた台車の加速度の時間変化をグラフにすると次のようになります。

加速も減速も時間\(t_1\)をかけ,等速でいる時間は\(t_2-t_1\)です。このグラフと初速ゼロという情報から,時刻\(t\)における台車の速度\(v\)は次のようになります。
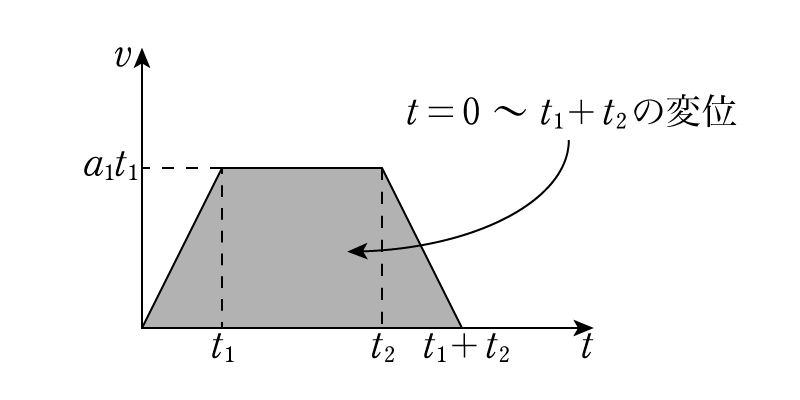
加速時の加速度は\(a_1\)ですから,速度の最大値は\(a_1t_1\)となります。また,\(v-t\)グラフの囲む面積が変位ですから,時刻\(t=0\)から\(t=t_1+t_2\)の間に移動した距離は図の灰色の部分の面積に等しく,\[ \dfrac{1}{2} \cdot a_1t_1 \cdot \{ (t_2-t_1)+(t_1+t_2) \} = a_1t_1t_2 \]となります。
したがってこの問題の答えは次の通りです。
時刻\(t=t_1\)における台車の速度 \(a_1t_1\)
時刻\(t=0\)から時刻\(t=t_1+t_2\)までの間に台車が移動する距離 \(a_1t_1t_2\)
小問(2)
ここでは,台車の加速度\(a\)があるときに物体の座標系では慣性力\(-ma\)がかかることに着目します。バネの伸びは\(y\)とかけるから,物体の加速度を\(a_y\)と書けば,それぞれの時間での物体の運動方程式は次のようになります。
- 加速時:\(ma_y=-ky-ma_1\)
- 等速時:\(ma_y=-ky\)
- 減速時:\(ma_y=-ky+ma_1\)
全て振動を表す方程式ですが,加速時と減速時はそれぞれ
- 加速時:\(ma_y=-k\left(y+\dfrac{ma_1}{k}\right)\)
- 減速時:\(ma_y=-k\left(y-\dfrac{ma_1}{k}\right)\)
と変形できるから,加速度がゼロになる振動中心は,加速時は\(y=-ma_1/k\)で減速時は\(y=ma_1/k\)であることがわかります。もちろん等速時は\(y=0\)を中心とする単振動となります。これを使って,\(y-t\)グラフ(位置と時間のグラフ)を書いていきます。
初期条件は物体の位置・初速度ともにゼロというものですから,\(y-t\)グラフは\(t=0\)で傾きがゼロで原点を通ります。また\(t=0\)から負の方向に慣性力を受けるのでグラフは負の方向に進んでいくはずです。加えて,加速時間は振動周期\(T\)の半分だから,グラフは次のように定まります。
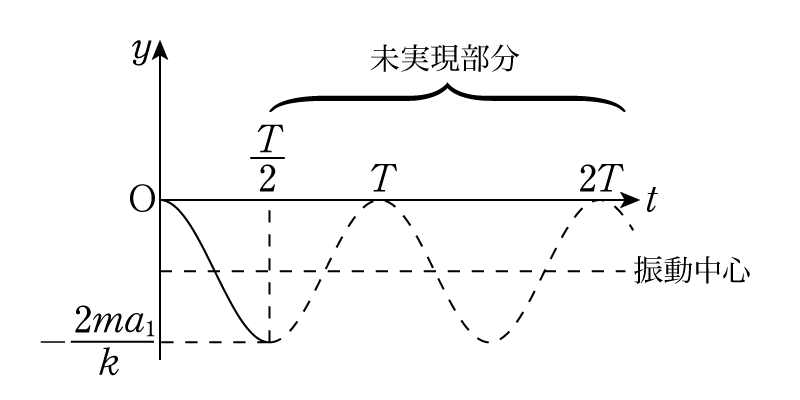
これを数式で表記するなら,\[ y=\dfrac{ma_1}{k}\left\{\cos\left(\dfrac{2\pi t}{T}\right)-1\right\}\]となります。ただし\(t>T/2\)では運動方程式が異なるため,このグラフのようにはなりません。
次に台車が等速運動している場合を考えます。このとき慣性力はありませんから,\(y=0\)を中心とするグラフとなりますが,\(0<t<T/2\)でのグラフと滑らかに繋がらなければいけないため,必然的に次のようになります。
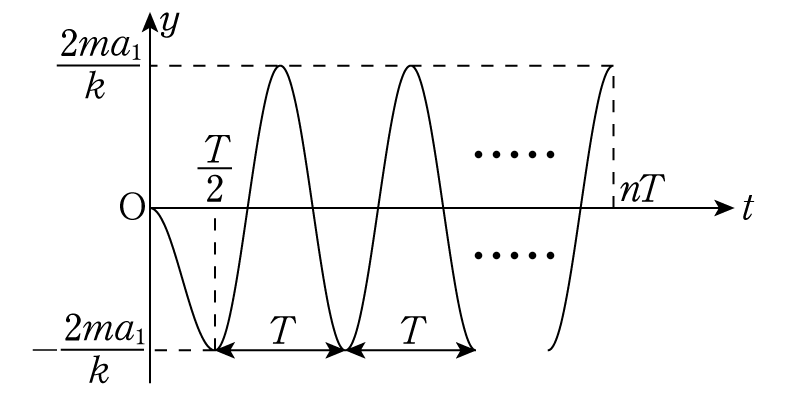
単振動の周期が\(T\)だから,\(t=nT\)においてはゼロ位置中心の振動が\(n-\dfrac{1}{2}\)回起こったところとなります。したがって,\(t=nT\)では\(y=\dfrac{2ma_1}{k}\)にいて,この座標での速度はゼロです。
最後にここに台車減速時のグラフを付け加えます。例によって,滑らかにグラフが繋がるようにして\(y=\dfrac{ma_1}{k}\)を中心とする振動を半周期だけ書けば良いから,次のようになります。
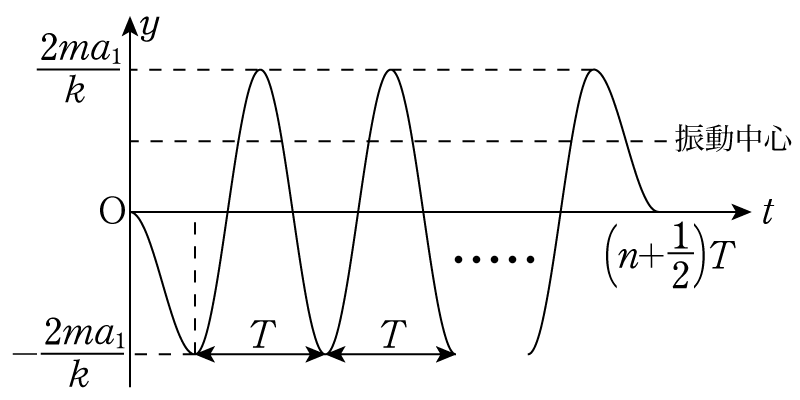
したがって,\(t=t_1+t_2=\left(n+\dfrac{1}{2}\right)T\)での位置はゼロで,相対速度もグラフの傾きよりゼロだとわかります。
小問(3)
(2)と同じように,加速時と減速時それぞれ運動方程式を立てます。
- 加速時:\(ma_y=-k\left(y+\dfrac{ma_2}{k}\right)\)
- 減速時:\(ma_y=-k\left(y-\dfrac{ma_2}{k}\right)\)
先ほどの\(a_1\)を\(a_2\)に変えればいいですね。ただし今回の初期条件は\(y=y_0\)で,相対速度がゼロというものですから,\(y-t\)グラフは傾きゼロでスタートしますがその位置がマイナスにずれます。そのため,振動中心である\(-ma_2/k\)と\(y_0\)の大小関係がまだわからず,グラフを書こうにも書けませんから,ここは数学的に処理してしまいましょう。
\(t=0\)で\(y=y_0\)かつ非慣性系での速度\(v_y=0\)となり,運動方程式\[ a_y =-\dfrac{k}{m} \left(y+\dfrac{ma_2}{k}\right) \]を満たす解は,\[y(t)=-\dfrac{ma_2}{k} + \left( \dfrac{ma_2}{k}+y_0 \right) \cos\left(\dfrac{2\pi t}{T}\right)\]となります。この式から,\(t=T/2\)での\(y\)座標は\[ y\left(\dfrac{T}{2}\right)=-\dfrac{2ma_2}{k}-y_0\]とわかります。
したがって,減速時については\(t=T/2\)で相対速度ゼロでかつ\(y\)座標は上で求めた\(y\left(\dfrac{T}{2}\right)\)となるように位置座標を定めれば良いです。計算すると,\[y(t)=\dfrac{ma_2}{k} + \left(\dfrac{3ma_2}{k}+y_0\right) \cos\left(\dfrac{2\pi t}{T}\right) \]とわかります。ゆえに,時刻\(t=T\)での位置座標は,\[y(T) = \dfrac{4ma_2}{k}+y_0\]となりますが,これがゼロになる条件を問われているから,\[a_2=-\dfrac{ky_0}{4m}\]とすれば良いことがわかりました。これを上で求めた\(y\left(\dfrac{T}{2}\right)\)に代入して,\[y\left(\dfrac{T}{2}\right)=-\dfrac{y_0}{2}\]だとわかりました。ここまでの議論をもとに,\(y-t\)グラフをかくと次のようになります。
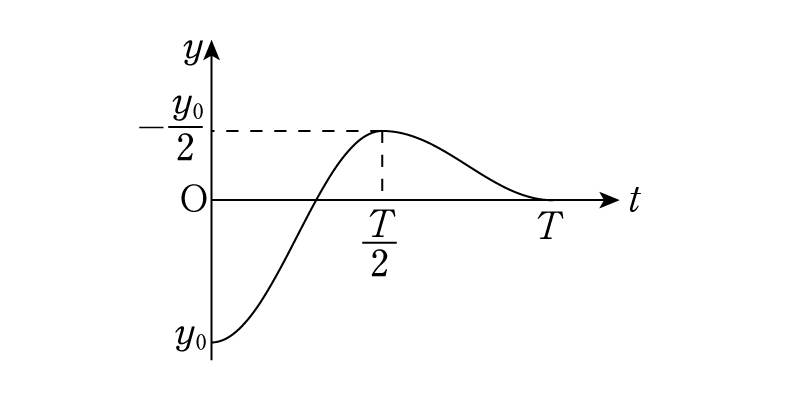
加速時と減速時では,振動中心・振幅が変わるので少しややこしい問題ですが,同じバネを使っている以上周期は変わらず,半周期ごとに相対速度がゼロになることを忘れなければ取り組みやすいと思います。
設問Ⅱ
倒立振子という見慣れない問題設定ですが,やることは先の設問同様に慣性力を考慮して微小角度の振動を考えるだけです。後半の誘導が少しめんどくさい気もします。
小問(1)
これは単に,重力と慣性力の棒に垂直な成分を取り出せば良いだけの話です。一応それぞれの力を分解してみると次のようになります。

したがって,正の向きに注意して\[ f=mg\sin\theta-ma\cos\theta\]となりますが,与えられた近似式を用いて,答えは次のようになります。\[f=mg\theta-ma\]
小問(2)
さて,ここは誘導に従って1つ1つ求めていく必要があります。これは振り子なので,周期は\[T=2\pi\sqrt{\dfrac{l}{g}}\]となります。これは問題中特に言及されていませんが,まあ当たり前のこと過ぎて聞いてないんですかね…。
まず\(t=0\)〜\(T/2\)での\(\theta\)は,\[\theta(t)=\dfrac{\theta_0-\theta_1}{2}\cos\sqrt{\dfrac{g}{l}}t + \dfrac{\theta_0+\theta_1}{2}\]となります。これはよく考えれば,「ア」が振幅,「イ」が振動中心ですから,グラフを見れば一瞬でわかりますね。
さてこのような運動をするために必要な力\(F\)が聞かれていますが,これは運動方程式に立ち返れば良いです。今回物体の加速度は\(l\dfrac{d^2 \theta}{dt^2}\)となりますから,運動方程式は\[ml\dfrac{d^2 \theta}{dt^2} = F\]です。実際に上の\(\theta\)を微分して求めると,\[F=-mg\dfrac{\theta_0-\theta_1}{2} \cos\sqrt{\dfrac{g}{l}}t\]です。ここに,\[\cos\sqrt{\dfrac{g}{l}}t = \dfrac{2}{\theta_0-\theta_1}\left( \theta-\dfrac{\theta_0+\theta_1}{2}\right)\]を代入すると,\[F=-mg\left(\theta-\dfrac{\theta_0+\theta_1}{2}\right)\]と求まります。これと(1)の\(f\)が等しいとすれば,\[mg\theta-ma=-mg\dfrac{\theta_0-\theta_1}{2} \cos\sqrt{\dfrac{g}{l}}t\]となるから,\(a\)について整理して,\[a=\left(\dfrac{\theta_0-\theta_1}{2} \cos\sqrt{\dfrac{g}{l}}t + \theta \right)g\]となります。最後にもう一回,上で求めた\(\theta\)の式を代入して,\[a=\left((\theta_0-\theta_1)\cos\sqrt{\dfrac{g}{l}}t +\dfrac{\theta_0+\theta_1}{2} \right)g\]となります。ややこしそうに見えますが,やっていることは微分と出てきた式の代入の繰り返しにすぎません。何をやっているのか見失わなければ大丈夫かなと思います。
さて,少し話が変わって台車の速度変化に着目します。加速度\(a\)の第1項は単振動に相当しますが,単振動では半周期ごとに速度がゼロになります。よって時刻\(t=0\)から\(t=T/2\)の速度変化に第1項は寄与せず,第2項のみ考えれば良いことがわかります。第2項は定数ですから,等加速度運動に相当し,速度変化は加速度×時間で求められます。ゆえに,\[v_1= \dfrac{\theta_0+\theta_1}{2} \cdot \dfrac{T}{2} \cdot g = \dfrac{(\theta_0+\theta_1)\pi\sqrt{gl}}{2}\]が答えです。
次に\(T/2<t<T\)での運動を考えます。先ほどと同じように考えると,この時間での\(\theta\)は振幅が\(-\theta_1/2\),振動中心が\(\theta_1/2\)の振動をしています(\(\theta_1<0\)に注意!)。これを数学的に表記すると,\[\theta(t)=\dfrac{\theta_1}{2}-\dfrac{\theta_1}{2}\cos\sqrt{\dfrac{g}{l}}t\]となります。同じように考えると,この振動を作り出す力\(F\)は\[F=-mg\left(\theta-\dfrac{\theta_1}{2}\right)\]だから,これと\(f\)が等しいとして,\[mg\theta-ma=-mg\left(\theta-\dfrac{\theta_1}{2}\right)\]よって\[a=\left(-\theta_1 \cos\sqrt{\dfrac{g}{l}}t+\dfrac{\theta_1}{2}\right)g\]となります。例によって,第1項は半周期の速度変化に無関係ないので,第2項だけ考えて,\[v_2=\dfrac{\theta_1}{2} \cdot \dfrac{T}{2} \cdot g = \dfrac{\theta_1\pi\sqrt{gl}}{2}\]です。
最後に,最初止まっていた台車が時刻\(t=T\)でも静止するためには,全体の速度変化がゼロである必要があります。つまり,\[v_1+v_2=0\]が必要だから,これに先に求めた結果を代入して,\[\dfrac{(\theta_0+2\theta_1)\pi\sqrt{gl}}{2}=0\]より,\[\theta_1=-\dfrac{\theta_0}{2}\]となります。

コメント