物理において超強力な数学的手法「フーリエ変換」。厳密な数学的定義はそこそこにして,微分方程式等々における適用例を見ながら使いこなせるようになりましょう。
フーリエ変換の定義
定義は教科書によって異なりますが,定数倍違うだけで本質的な意味はどれも同じです。
\[ \hat{f}(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i\omega t} \, dt \]
\[ f(t) = \dfrac{1}{2\pi} \int_{-\infty}^{\infty} \hat{f}(\omega) e^{i\omega t} \, d\omega \]
フーリエ変換の物理的意味
変換の式を見て「これは一体何の意味があって何の役に立つんだ」と思った人も多いかと思います。この物理的解釈を最初に理解するのはかなり難しいと思うので(私も最初見たときは全然意味はわかりませんでした)問題にあたって使っていくうちに理解していけばよいと思います。
とは言うものの,一応それっぽいことを書いておきます。どのような関数でも正弦関数と余弦関数を適当に定数倍して足し合わせることで表現できる(フーリエの定理)ことが知られています。この時足し合わせるのは,様々な(理論上は無限の種類の)周波数をもつ三角関数を足し合わせる必要があります。例えば高校で出てくる3倍角の公式\[ \cos^3(t) = \dfrac{1}{4} \cos(3t) + \dfrac{3}{4} \cos(t) \] も,左辺の関数を周波数\(\dfrac{1}{2\pi}\)の関数である\(\cos(t)\)と周波数\(\dfrac{3}{2\pi}\)の関数である\(\cos(3t)\)を使って表現した,ということができます。
このような時,関数を分解したときのそれぞれの周波数の寄与度は係数で表現できそうですよね。つまり先の例での\(\cos^3(t)\)は,周波数\(\dfrac{1}{2\pi}\)の寄与が\(\dfrac{3}{4} \),周波数\(\dfrac{3}{2\pi}\)の寄与が\(\dfrac{1}{4} \)ということができます。つまり,時刻\(t\)で関数を表現する代わりに,周波数\(\omega\)の寄与度で表現しているわけです。時間によって変化するある関数やデータにおいて,どの周波数からの寄与が大きいかを調べることをスペクトル解析と言ったりもして,幅広い分野で用いられています。
フーリエ変換の数学的性質
この変換の解釈はこの位にしておいて,数学的な性質をチェックしていきましょう。いちいち積分記号を書くのも面倒なので\(f(t)\)から\(\hat{f}(\omega)\)への変換を\[ \hat{f}(\omega) = \mathcal{F}[f(t)] \]と書くことにしましょう。まず,これは線型変換ですから線型性
\[ \mathcal{F}[af+bg] = a\hat{f} + b\hat{g} \]
が成り立ちます。つまり,足し算されていればそれぞれ変換すればよいし,定数倍はそのままで良いということです。さらに\(f\)の微分\(f’\)のフーリエ変換は
\[ \mathcal{F}[f'(t)] = i\omega\hat{f}(\omega) \]
と書けます。これは非常に便利で,微分のフーリエ変換は元の関数のフーリエ変換の\(i\omega\)倍となります。次に,元の関数を時間方向に\(a\)倍縮めたものの変換は
\[ \mathcal{F}[f(at)] = \dfrac{1}{|a|}\hat{f}\left(\dfrac{\omega}{a}\right) \]
となる。中身も外身も\(1/a\)倍と押さえておけば良いでしょう。最後に,元の関数を時間方向に\(a\)だけ平行移動させたものの変換は
\[ \mathcal{F}[f(t-a)] = e^{-i\omega a}\hat{f}(\omega) \]
である。手前に余計な係数がくっついてきますが,覚えてあげましょう。
物理で出てくる微分方程式への応用
さてフーリエ変換そのものに興味がある人は専門書等をあたってもらえれば無限に詳しく書かれていますが,これからは物理学におけるツールとしてのフーリエ変換を見ていきましょう。最もシンプルな例として,ばねの単振動を考えてみましょう。運動方程式は
\[ \dfrac{d^2 x(t)}{dt^2} = -\dfrac{k}{m}x(t) \]
であったはずです。ここで両辺をフーリエ変換すると,左辺は2階微分ですから\((i\omega)^2\)が係数として出てきます。つまり
\[ -\omega^2 \hat{x}(\omega) = -\dfrac{k}{m} \hat{x}(\omega) \]
ですから\( \omega=\pm\sqrt{\dfrac{k}{m}}\)ということがわかりました。これは単振動の固有振動数に他なりませんね。マイナスの周波数というのは直感的には理解できませんが,数学的に出てきたことなのでとりあえず受け入れて前に進みましょう。\(\omega\)が正負合わせて2個しか出てこなかったわけだから,この関数\(x(t)\)はこの2つの周波数のみで記述できるということになります。したがって
\[ x(t) = A\exp\left(i\sqrt{\dfrac{k}{m}}t\right) + B\exp\left(-i\sqrt{\dfrac{k}{m}}t\right) \]
と書くことができます。周波数\(\omega\)の振動は\(e^{i\omega t}\)と書くんでしたね。三角関数で書けば
\[ x(t) = (A+B)\cos \omega t + i(A-B) \sin \omega t \]
です。もちろん\(A\)や\(B\)は複素数で状況によって決まる定数です。最終的にこれの実部を取れば実際のばねの位置座標を求めることができます。いずれにせよ,ばねの単振動が三角関数で記述できることが確認できましたね。他にも多様な応用方法がありますが,それぞれの状況ごとに説明ページを書いていきたいと思いますので,そちらを参照していただければと思います。
特別な関数のフーリエ変換
一般の関数のフーリエ変換はそう簡単に求まりませんが,ここでは頭に入れておきたいいくつかの有名なフーリエ変換を紹介します。
デルタ関数
\(t=\tau\)で無限大のピークを持つデルタ関数\(\delta(t-\tau)\)を考えましょう。この変換は
\[ \hat{f}(\omega) = \int_{-\infty}^{\infty} \delta(t-\tau) e^{-i\omega t} \, dt = e^{-i\tau\omega} \]
となります。デルタ関数の性質からほとんど明らかですが,単なる振動解がでてきます。特に\(\tau=0\)とすれば,
\[ \mathcal{F}[\delta(t)] = e^0 = 1 \]
となります。したがって,逆に考えれば1のフーリエ逆変換はデルタ関数\(\delta(t)\)だということになります。これを式にすると,
\[ \dfrac{1}{2\pi} \int_{-\infty}^{\infty} 1\cdot e^{i\omega t} \, d\omega = \delta(t) \]
ですが,左辺の積分において\(\omega\)を\(-\omega\)と書き換えても数学的に値は変わりません。それを両辺\(2\pi\)倍すれば,
\[ \int_{-\infty}^{\infty} 1\cdot e^{-i\omega t} \, d\omega = 2\pi\delta(t) \]
となります。別に\(\omega\)と\(t\)はどっちがどっちでも良いわけだから入れ替えて,
\[ \int_{-\infty}^{\infty} 1\cdot e^{-i\omega t} \, dt = 2\pi\delta(\omega) \]
を得ます。これは1のフーリエ変換がデルタ関数になることを意味しています。
カーディナル・サイン
いきなりですが\(\hat{f}(\omega)=1\)のフーリエ逆変換を\(-\omega_0<\omega<\omega_0\)の間だけ考えることにしましょう。
\begin{align*}
f(t) &= \dfrac{1}{2\pi}\int_{-\omega_0}^{\omega_0} e^{-i\omega t}\, d\omega
= \left[ \dfrac{ e^{-i\omega t}}{-it} \right]_{-\omega_0}^{\omega_0} \\
&= \dfrac{e^{i\omega_0 t}-e^{-i\omega_0 t}}{2\pi it}
= \dfrac{\sin \omega_0 t}{\pi t}
\end{align*}
となります。この最後の関数は非常に有名でカーディナル・サインと呼ばれ工学系の信号処理の分野で頻繁に出てきます。これを逆手にとって\(f(t)= \dfrac{\sin\omega_0 t}{t}\)のフーリエ変換は
\begin{eqnarray*}
\int_{-\infty}^{\infty} \dfrac{\sin\omega_0 t}{t} = \begin{cases}
\pi \quad (|\omega| < \omega_0) \\
0 \quad (それ以外) \end{cases} \end{eqnarray*}
となりますから,矩形パルスが出てきました。ちょっと解釈をしてみると,これはつまりカーディナル・サインは周波数の絶対値が\(\omega_0\)より小さい成分だけを持ち,それより周波数の大きい成分は全くもたないと言えます。このことが、この関数がバンドパスフィルタと呼ばれる所以で,この関数を使うことにより解析したいデータのうち小さな周波数成分だけを取りだすといったことが可能になります。この変換をグラフで表すと以下のようにになります。
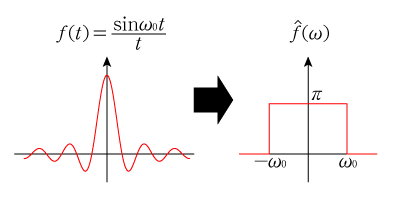
特に工学系を学んでいる人は必ず頭に入れておくべき内容ですので,導出も含めしっかり理解しましょう。
ガウス関数
最後に超有名なガウシアンをやってみましょう。\( f(t)=e^{-at^2} \)というシンプルな例でやることにします。変換の式にいれてガツガツ計算していきましょう。
\hat{f}(\omega) &= \int_{-\infty}^{\infty} e^{-at^2} \cdot e^{-i\omega t}\, dt = \int_{-\infty}^{\infty} e^{-at^2-i\omega t} \, dt \\
&= \int_{-\infty}^{\infty} \exp \left\{ -a\left(t+\dfrac{i\omega}{2a} \right)^2 – \dfrac{\omega^2}{4a} \right\} dt \\
&= \exp \left( -\dfrac{\omega^2}{4a} \right) \int_{-\infty}^{\infty} \exp \left\{ -a\left(t+\dfrac{i\omega}{2a} \right)^2 \right\}dt
\end{align*}
となります。指数部分を平方完成するところがミソですが,汚くなるので\(\exp\)を用いて表記しました。さて,残りの積分ですが,これはガウス積分の公式

コメント