高校の熱力学において最も大事な式である熱力学第一法則。気体の状態変化を追うときに必要な式ですから,計算だけでなく意味もしっかり理解して使えるようにしましょう。
気体の内部エネルギーとは
熱力学第一法則を語る前に,気体の内部エネルギーという量を導入する必要があります。別ページに詳しく記載しますので,ここでは軽く導入します。
物理でエネルギーという概念を習えば,まあ気体だって何となくエネルギーがあるんだろうなぁ,位には思うかもしれません。そう,気体にもエネルギーはあります。運動エネルギーとか位置エネルギーとか習ってきたと思いますが,気体の場合は内部エネルギーと呼びます。
でもこれ,全くもって新しいもの,ということでは実はないんです。中学校でやったかもしれませんが,気体というのは気体分子が自由に飛び回っている状態でしたよね。イメージとしてはこんな感じです。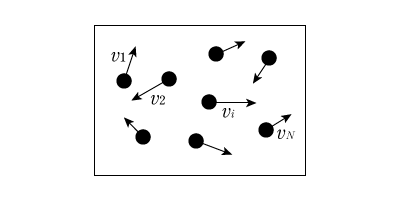
箱の中に気体分子(黒丸)が\(N\)個入っていて,それぞれがそれぞれの速さ\(v_i\)を持っています。みんながみんな同じ速さで動いているとは考え難いですもんね。このとき気体分子の質量を\(m\)とすると,\(i\)番目の分子の運動エネルギーは
\[ \dfrac{1}{2}m{v_i}^2 \]
と書けます。これを1番目から\(N\)番目まで足し合わせると,運動エネルギーの合計値になりますが,実はこれが気体の内部エネルギーの正体です。結局,内部エネルギー\(U\)は次のように決まります。
\[ U = nC_VT \]と書ける。ここで\(C_V\)は定積モル比熱という気体ごとの定数。
エネルギーの変化を追ってみる
さて力学ではエネルギーが変化するためには,何が必要だったでしょうか。「力」では不正解です。「仕事=力×変位」が必要でしたよね。その考えは熱力学でも同じです。気体の内部エネルギーを変化させるには仕事を加えてやる必要があります。またそもそもエネルギーとは何か仕事をする能力を表す量でしたから,
- 気体自身が仕事をしたら,内部エネルギーは減少する
- 気体自身が仕事を受けたら,内部エネルギーは増える
と考えることができますよね。気体がする仕事を\( W_{\text{out}} \)と書くことにすると,エネルギー変化\( \Delta U\)は
\[ \Delta U = -W_{\text{out}} \]
と書くことが出来そうですね。気体自身が外部に仕事をするとエネルギーが減ってしまうわけだから,マイナスの符号がつきます。
ですが,これでOKなのでしょうか。実は気体の内部エネルギー変化は仕事だけによって引き起こされるのではありません。色々実験してみると,仕事をしてもいないのにエネルギーが増えている,ということも起こりうることがわかったのです。これでは,上の式では辻褄が合いませんから,帳尻合わせでもってよくわかりませんが,上の式の右辺(エネルギー変化の原因)にもう一つ「熱」という項を付け加えることにしましょう。
\[ \Delta U = -W_{\text{out}} + Q_{\text{in}} \]
- 仕事をしたり,熱が出ていくと減少する
- 仕事をされたり,熱が入ってくると増加する
ということにあります。たまにこの式の添字を略して書かない人がいますが,それは絶対にダメです。単に\(Q\)などと書かれても,それが入ってきた熱なのか出ていった熱なのかわからないからです。高校物理の段階では,この熱力学第一法則によって「熱」という量を初めて定量的に定義できることになります。つまり,
物理量を用いた具体的表記
さてこれで熱力学第一法則の意味はわかったと思います。ただこれでは実用上の計算が何も出来ませんからそれぞれの項を書き下していきましょう。ただし熱の項\(Q_{\text{in}}\)は熱力学特有の項なのでどうすることも出来ません。
エネルギー変化の項 \(\Delta U\)
エネルギーは絶対温度にのみ比例するということがわかっています。物質量は普通は変化しませんから,エネルギーが変化するということは温度が変化する,ということになります。ですから,第一法則の左辺は次のように書き換えられます。
\[ \Delta U = nC_V \Delta T \]
仕事の項 \(W_{\text{out}}\)
力学でやる通り,仕事は力と変位の積で表されます。より正確には力と変位は共にベクトル量ですから,その内積が仕事ですがここでは簡単のため力×変位ということにします。次のようなシチュエーションを考えてみましょう。

圧力が\(p\)である気体を箱に入れて,灰色の壁でもって右側から蓋をしています。この箱の断面積(灰色の蓋も同じ面積)は\(S\)です。何らかの理由で,気体の圧力が壁を押すことによって壁が右側に\(x\)だけずれたとしましょう。
このとき気体が壁を押す力\(F\)は\(pS\)です。これは圧力が単位面積当たりの力であることから分かります。すると気体のした仕事は\(Fx\)ですから,
\[ W_{\text{out}} = Fx = pSx \]
です。ところで,この最後の\(Sx\)という値ですが,見方を変えれば断面積×横なので,体積の増加分ということになります。図で言うと灰色の壁で囲まれた部分の体積に相当します。体積の増加分なのでこれを\(\Delta V\)と書くと,
まとめ
以上の考察から,熱力学第一法則は
\[ \Delta U = -W_{\text{out}} + Q_{\text{in}} \]
と書くか,物理量をあらわにして書けば
\[ nC_V\Delta T = -p\Delta V + Q_{\text{in}} \]
とも表現できます。どちらにしても使いこなせるようにしていきましょう。この法則は気体の状態が変化した際に,それがどのように変化したのかを決定できる強力なツールです。高校で学ぶ4種類の状態変化に対して適用しますが,それは別ページにてまとめる予定です。
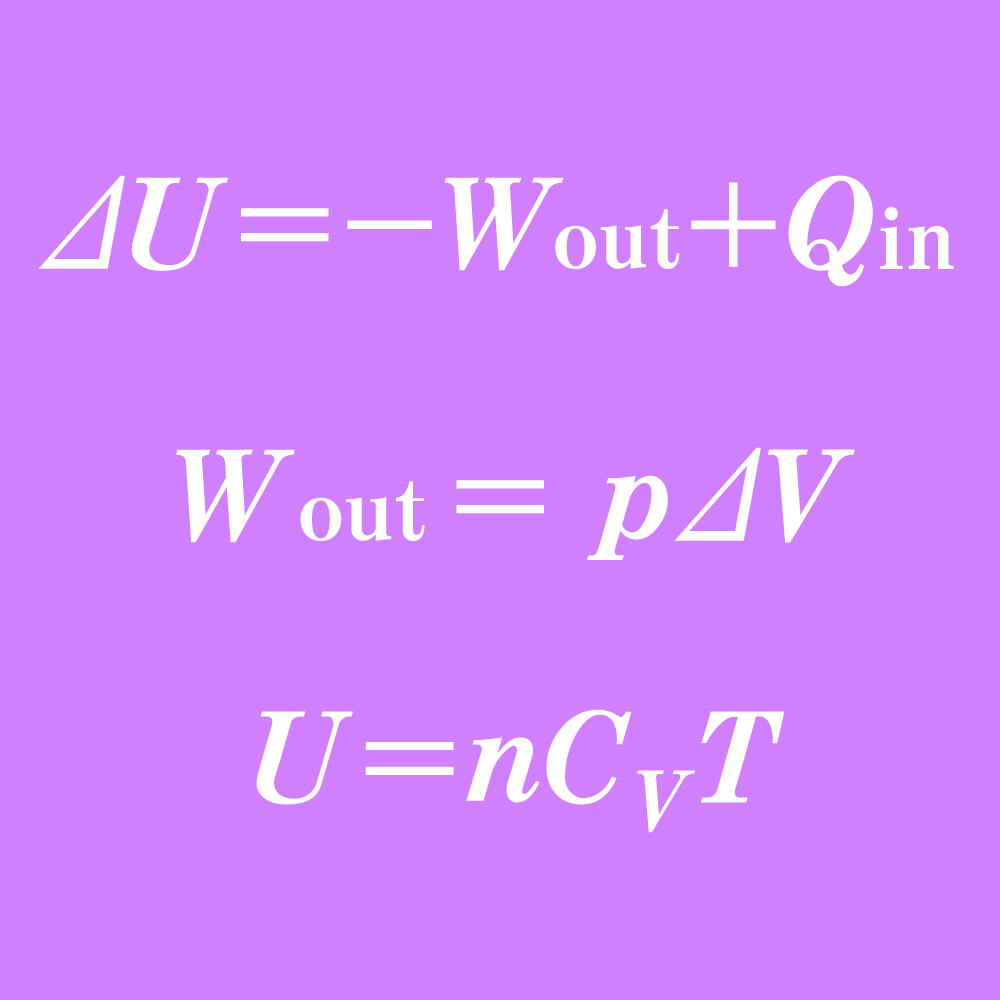
コメント